Пример
2.3.7. Решить уравнение![]()
Решение
|
Поскольку |
|
|
то имеем
![]()
![]()
Следовательно,
![]()
|
Обозначая |
|
получим |
![]()
![]()
Методом подбора легко найти корень уравнения
t = –1.![]()
![]()
Используя метод неопределенных коэффициентов, получим
|
|
|
|
Итак, |
|
|
Решая уравнение |
|
найдем |
t = 6, t = 16
Следовательно, исходное уравнение равносильно совокупности трех квадратных уравнений
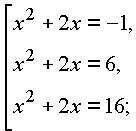
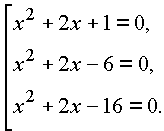
|
Поскольку |
|
то первое уравнение имеет двукратный |
|
|
корень x = –1. Второе и третье уравнения соответственно имеют корни |
|||
|
|
|
||
|
Ответ: |
|
|
|
|
|