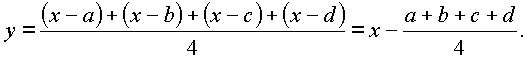
Указание
@
Уравнения вида(x – a)(x – b)(x – c)(x – d) = A
,где
a < b < c < d, b – a = d – c, можно решать, используя симметризацию уравнения (замену переменных)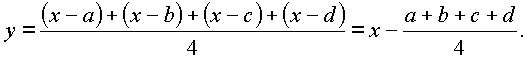
Пример
2.3.6. Решить уравнение(x + 1)(x + 2)(x + 3)(x + 4) = 24
.Решение
1 способ.
(x – (–4))(x – (–3))(x – (–2))(x – (–1)) = 24.Так как
–4 < –3 < –2 < –1 и (–3) – (–4) = (–1) – (–2), то введем новую переменную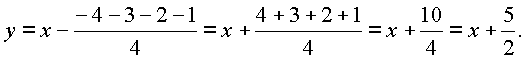
|
Подставляя |
|
в исходное уравнение, получим |
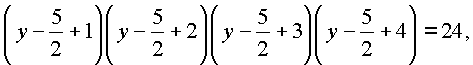
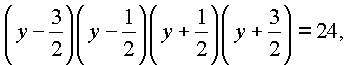
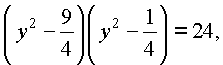
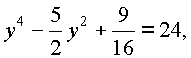
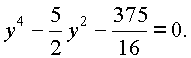
Пусть
y2 = z > 0, тогда![]()
Корнями этого уравнения являются
|
|
|
(не удовлетворяет условию). |
|
Следовательно, |
|
Возвращаясь к исходной неизвестной, получим
|
|
или |
|
2 способ.
Перепишем уравнение в виде![]() ,
,
![]()
|
Обозначая |
|
получим |
![]()
|
|
откуда |
|
|
|
Возвращаясь к исходной неизвестной, получим совокупность двух уравнений
|
|
или |
|
|
Уравнение |
|
действительных корней не имеет. |
|
Уравнение |
|
имеет два корня |
|
|
Ответ: –5; 0.