Указание
@
Уравнения вида![]()
|
|
|
|
можно решать, полагая в первом уравнении |
|
а во втором |
|
|
|
предварительно разделив обе части этих уравнений на x2 |
||
(x = 0 не является корнем ни первого, ни второго уравнений).
|
Поскольку |
|
|
то, используя |
|
Несложные преобразования, получим |
|||
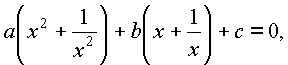
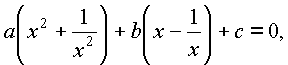
|
|
|
||
|
или |
|
|
(* ) |
Таким образом, если
u1, u2 – корни первого уравнения, а v1, v2 – корни второго уравнения, то исходные уравнения равносильны соответственно совокупностям уравнений|
|
|
Если квадратные уравнения
(*) решений не имеют, то исходные уравнения также не имеют решений.Пример
2.3.3. Решить уравнение![]()
Решение
Поделив обе части уравнения на
x2 (x = 0 не является корнем уравнения), получим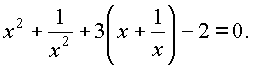
Полагая
x + 1/x = t, получим![]()
![]()
Решая квадратное уравнение, найдем его корни
t = –4, t = 1, следовательно,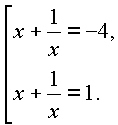
|
откуда |
|
или |
|
|
Действительные корни имеет только первое из полученных уравнений: |
![]()
|
Ответ: |
|