Указание
@
Решение показательных уравнений вида![]()
|
где |
|
– некоторая функция, основания степеней |
a
, b, c, – последовательные члены геометрической прогрессии, т.е. b2 = ac, сводится к решению квадратных уравнений путем замены переменной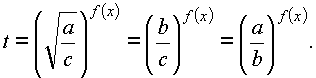
Получим
![]()
Если это уравнение имеет корни
t1 и t2, то решение уравнения сводится к решению совокупности показательных уравнений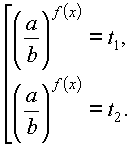
Пример
2.6.2. Решить уравнение![]()
Решение
|
Так как |
|
то обозначим |
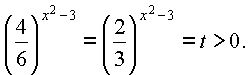
|
Получим квадратное уравнение |
|
корнями которого являются |
t
= –2 (не удовлетворяет условию), t = 2/3.|
Откуда |
|
Решая показательное уравнение, получим
|
|
|
т.е. |
|
Ответ:
–2; 2.