Пример
2.7.9. Решить уравнение ![]()
Решение
Переходя к новому основанию логарифмов, например, 3 (хотя, заманчивым кажется в роли нового основания и само неизвестное
x, но об этом сделаем особое замечание в конце решения), имеем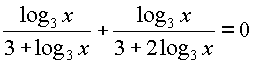 .
.
|
После замены |
|
получим y(y + 2) = 0. Очевидные корни последнего |
уравнения
y1 = 0, y2 = –2 позволяют выписать и решения исходного уравнения x1 = 1, x2 = 1/9.Что касается перехода к новому основанию, содержащему неизвестное, то этого лучше не делать, так как каждый раз приходится следить за тем, при каких
x преобразование возможно, проверяя при этом непосредственной подстановкой в исходное уравнение те значения x, при которых основание логарифмов отрицательно или равно 1. В данном случае, переходя к новому основанию x, мы вынуждены запретить неизвестному быть равным 1, хотя по условию этого запрета нет, и более того, x = 1 является очевидным решением исходного уравнения. И, чтобы не потерять это решение, мы, установив факт, что x = 1 является решением исходного уравнения, ищем другие решения, отличные от x = 1. Тогда потери решения не произойдет и оставшееся решение x = 1/9 будет найдено обычным способом из уравнения![]()