Пример 2

Пример 2.7.8. Решить уравнение

Решение

Исходное уравнение равносильно следующей системе

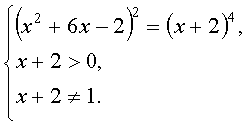
Первое уравнение этой системы можно было бы решать непосредственным возведением обеих его частей в указанную степень с дальнейшим приведением подобных. Но от необходимости решения кубического уравнения нам не уйти. Хорошо, если среди делителей свободного члена кубического уравнения

есть его очевидный корень (очевидно решение),

тогда решить квадратное уравнение не составляет особого труда.

т.е.

Проверка убеждает в том, что все три корня удовлетворяют исходному уравнению и всем требованиям эквивалентной системы.

Можно было бы исходное уравнение заменить и следующей системой, не требующей умения решать уравнения степени, большей двух

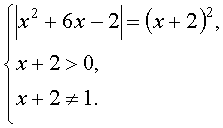
Далее решаем два квадратных уравнения

а)

b)

первое из которых дает x₁ = 3, а второе

Но самым целесообразным решением нам представляется следующее.

Первое уравнение полученной системы можно переписать так

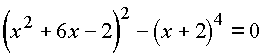
или

Отсюда получаются все ранее указанные корни.

Ответ: 3;