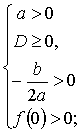
или
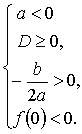
Пример
2.2. Найти все значения параметр а, квадратное уравнение(a –
2)x2 – 2ax + 2a – 3 = 0имеет два различных положительных корня.
Решение
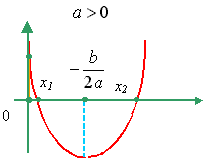
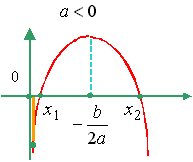
: Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были больше 0 (т.е. лежали на числовой оси правее 0), необходимо и достаточно выполнение условий:|
|
или |
|
|
|
|
|
В данном случае эти условия имеют вид (с учетом того, что
D > 0, когда a < 1 или a > 6)|
|
или |
|
|
Откуда получаем: |
||
|
a > 6 |
или |
a < 0 |
Самостоятельно разберите ситуации когда:
Задачи для самостоятельного решения
|
|
Условие |
Ответ |
|
1. |
Не решая квадратного уравнения, определить знаки его корней |
|
|
3x2 + 12x – 4 = 0 |
Корни разных знаков |
|
|
9x2 – 16x + 1 = 0 |
Оба положительны |
|
|
3x2 + 8x + 4 = 0 |
Оба корня отрицательны |
|
|
2. |
Найти все значения a, для которых уравнение x2 – 2(a – 1)x + (2a + 1) = 0 имеет два положительных корня. |
|
|
3. |
При каких значениях параметра а корни уравнения x2 – 2(а – 1)х + 2а + 1 = 0 имеют разные знаки и по абсолютной величине меньше 4. |
|
|
4. |
При каких значениях параметра а корни уравнения ax2 – (2a + 1)x + 3a – 1 = 0 больше 1? |
|