ПРИМЕР 7.4.3.
Решить уравнение.3sin5z - 2cos5z = 3
Решение:
Представим уравнение в виде![]()
И применив формулы: sin2
a = 2sina cosa и cos2a = cos2a -sin2a , запишем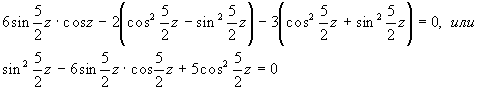
Это однородное уравнение 2-ой степени.
1 случай: cos(5z/2) = 0 следовательно уравнение примет вид sin
2(5z/2)=0 ⇒ sin(5z/2)=0. Но так как cos и sin одновременно не равны нулю( sin2z+cos2z=1
≠ 0), то решения уравнения cos(5z/2)=0 не являются решениями исходного уравнения.2 случай: cos(5z/2)
≠ 0. Разделив уравнение на cos2(5z/2)≠ 0, получим![]()
Решив уравнение как квадратное относительно tg(5z/2), найдем
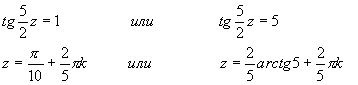
ОТВЕТ:
Список тригонометрических формул Содержание главы