ПРИМЕР 7.3.1.
Решить уравнение5sin2x-5cos2x=tgx+5
Решение:
Применив формулы ![]()
Представим заданное уравнение в виде
![]()
Обозначив tg x = t, запишем
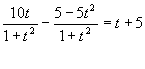
После приведения к общему знаменателю и несложных преобразований придем к уравнению t
3 – 9 t + 10 = 0. Один из делителей свободного члена, а именно t1=2, является корнем этого уравнения. Разложив левую часть на множители, получим (t - 2) (t2 + 2t - 5) = 0. Решив квадратное уравнение t2+2t-5=0, найдем еще два значения t2=√ 6-1, t3=-√6-1.Т.об. исходное уравнение равносильно совокупности трех уравнений
tgx = 2 x1 = arctg2+p n
tgx = √ 6-1 ⇒ x2 = arctg(√ 6-1)+π n, n∈ Z
tgx = -√ 6-1 x3 = - arctg(√ 6+1)+π n
ОТВЕТ:
arctg2+π n; arctg(√ 6-1)+π n; - arctg(√ 6+1)+π n, n∈ Z.Список тригонометрических формул Содержание раздела