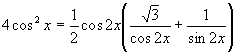
Упражнения для самостоятельного решения по теме "Метод
введения вспомогательного угла".
пример1 пример2 пример3 пример4 пример5 пример6 пример7 пимер8
список тригонометрических формул содержаните раздела
Решить уравнения:
. cos3x-sin3x = √ 3(cosx-sinx)
ответ:
x=π /8(4k+1), x=π /12(12k+1), k∈ Z . sin2z+cos2z = √ 2 sin3zответ:
z = π /4(8k+1), z = π /20(8k+3), k∈ Z sin3x+ √ 3/2sin5x+1/2cos5x = 0ответ
: x = 75° +180° k, x = 45° k-3° 45′ , k∈ Z sin8x – cos6x = √ 3(sin6x+cos8x)ответ:
x=π /4+π k, x = π /12+π k/7, k∈ Z. . sin10x+cos10x = √ 2sin15xответ:
x = - π /20- 2π n/5, x = 3π /100+2p n/25, n∈ Z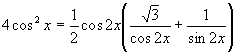
ответ:
x = π /12+π n, x = 5π /36+π n/3, n∈ Z. 4sin3x+3cos3x = 5,2ответ:
решений нет. sin3x+sin5x = 2(cos22x-sin23x)ответ:
x1=π /2(2n+1), x2=π /18(4k+1), n,k∈ Z sinx+cosx = 1ответ:
x=2π n, x = π /2(4n+1), n∈ Z