ПРИМЕР 7.2.3. Решить уравнение

sin2x + cos2x = √ 2 sin3x

Решение: Умножив обе части уравнения на √ 2/2, будем иметь

√ 2/2⋅ sin2x + √ 2/2⋅ cos2x = √ 2/2⋅ √ 2⋅ sin3x,

cos(π /4-2x) = sin3x,

cos(π /4-2x) – sin3x = 0

Поскольку cos(π /2-x) = sinx, запишем это уравнение в виде

cos(π /4-2x) - cos(π /2-3x) = 0

Преобразовав разность косинусов в произведение, получим

 

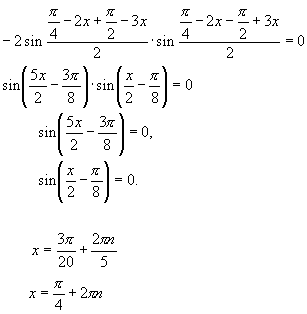
ОТВЕТ: x1=π /20(8n+3); x2=π/4(8n+1), n∈Z.

справка  меню