пример1 пример2 пример3 пример4 пример5 пример6 пример7 пимер8

пример9

Пример 1. sin²x-cos²x=cos(x/2)

ответ: х = 4/5(p/2+πk), x = 4/3(π/2+πk), k∈Z

ответ: x = pk, x = π/4(4k-1), k∈Z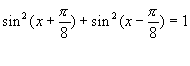

ответ: x = p /4(2k+1), k∈Z

Пример 4. cosx+cos2x = sinx+sin2x

ответ: x = p+2πk, k∈Z; x = π/6+2/3πk, k∈Z

Пример 5. cos3x=sin2x+cosx 

Пример 6. sinx+sin3x+sin5x=0

ответ: x = π /3k, k∈Z

Пример 7. sinx+cos4x = cos2x-sin5x

ответ: x₁=πn/3, x₂ = -π /2+2πn, x₃ = (-1)ⁿ π/6+pn, n∈Z

Пример 8. sinx⋅sin2x⋅ sin3x = ¹/₄sin4x

ответ: x₁ = πn/2, x₂ = π /8(2n+1), n∈Z

Пример 9. sin²2x+sin²3x+sin²4x+sin²5x = 2

ответ: x₁ = π/4 (2n+1), x₂ = p /14 (2n+1), n∈Z