Условия задачи
Уравнения
Если бы первый работал половину отведенного времени, второй – 1/3, а третий – 1/4, то они сделали бы 30 деталей
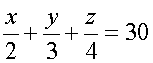
Если бы первый работал 1/6 часть отведенного времени, второй – 1/10, а третий 1/15, то они сделали бы 10 деталей
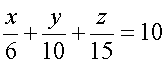
Пример
4.2.7. Трое рабочих должны сделать некоторое количество деталей. Если бы первый работал половину отведенного времени, второй – 1/3, а третий – 1/4, то они сделали бы 30 деталей. Если бы первый работал 1/6 часть отведенного времени, второй – 1/10, а третий 1/15, то они сделали бы 10 деталей. Какое количество деталей сделали бы трое рабочих вместе, если бы работали все отведенное время?Решение:
Пусть производительность первого рабочего x, второго – y, третьего z д/ед. времени. Время, которое они должны проработать, примем за единицу. Тогда искомое количество деталей N равно x + y + z.|
Условия задачи |
Уравнения |
|
Если бы первый работал половину отведенного времени, второй – 1/3, а третий – 1/4, то они сделали бы 30 деталей |
|
|
Если бы первый работал 1/6 часть отведенного времени, второй – 1/10, а третий 1/15, то они сделали бы 10 деталей |
|
|
Приходим к системе: |
|
Ясно, что если найдутся такие числа
u и v, для которых выполнено равенство:|
|
..., (1) |
то
N = 30u + 10vПриравнивая в (1) коэффициенты при неизвестных
x, y, z приходим к системе для u и v: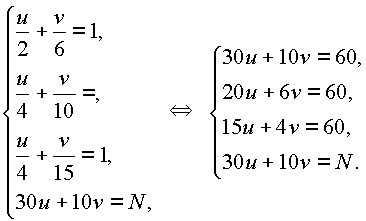
Из первого и последнего уравнений видно, что
N = 60 деталей. Нужно убедиться, что имеются такие u и v. Для этого можно найти их из первых двух уравнений и убедиться, что они удовлетворяют третьему. Таким образом, находим u = 12, v = -30.