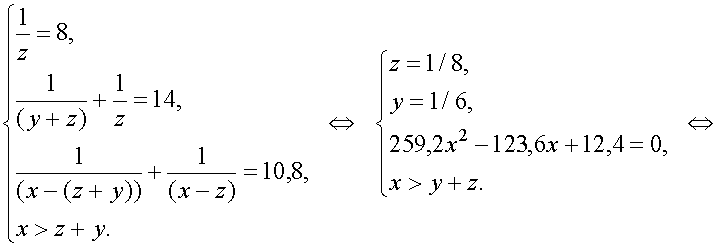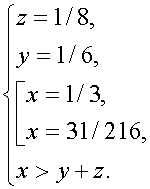Условия задачи
Уравнения
Если открыть только нижнюю трубу, то полный бак становится пустым за 8 часов
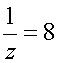
Если открыть и нижнюю, и боковую трубы, то полный бак опустошается за 7 часов
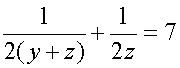
Если же в пустом баке открыть все три трубы, то он наполняется за 5 часов 24 минуты
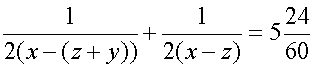
При этом ясно, что для того, чтобы в последнем случае бак наполнялся, необходимо чтобы через верхнюю трубу воды вливалось больше, чем через нижнюю и боковую за тоже время выливалось
![]()