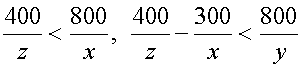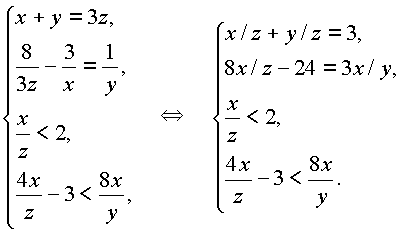Условия задачи
Уравнения
Первый и второй экскаваторы вместе вынимают за час грунта втрое больше, чем третий
![]()
Первый и третий экскаваторы начали работу одновременно, а второй – в тот момент, когда первый вынул уже 300 м
3 грунта, следовательно, он начал работать на 300/x позже первого и третьегоКогда третий экскаватор выполнил 2/3 своей работы, второй вынул 100 м
3 грунта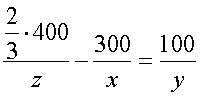
Первым выполнил свое задание третий экскаватор