Из прямоугольного треугольника
ACB по теореме Пифагора имеем![]()
, тогда
![]()
Из треугольника
![]()
имеем
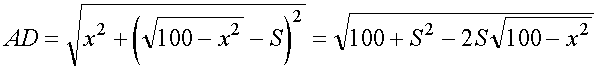 .
.
Пример
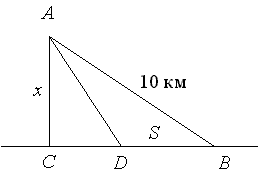
4.5.3. (КубГУ, ФПМ, предв., экз., 1992 г.) Пункт A расположен в поле на расстоянии от дороги, которая является прямой линией, здесь же находится пункт B; расстояние от A до B равно 10 км. Скорость движения автомобиля по дороге в три раза больше, чем по полю. Известно, что если ехать из A в B так, что часть пути проделать по дороге, то даже при самом удачном выборе пути движения на это уйдет не меньше времени, чем потребуется, если ехать напрямик по полю. Найти минимально возможное расстояние от A до дороги.Решение:
Обозначим расстояние от A до дороги через x, x < 10. D – точка, в которой автомобиль выезжает на дорогу. Пусть DB путь по дороге, пройденный автомобилем равен S км. Так как расстояние по прямой короче криволинейного пути, то будем полагать, что по полю автомобиль ехал по прямой AD.|
|
Из прямоугольного треугольника ACB по теореме Пифагора имеем |
||
|
|
, тогда |
|
|
|
Из треугольника |
|
имеем |
|
|
|
|||
Пусть скорость движения автомобиля по полю
V км/ч, тогда по дороге – 3V км/ч. По условию задачи имеем неравенство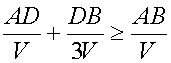 ,
,
и, в силу введенных обозначений, получим
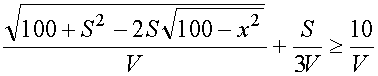 .
.
Так как
30 - S > 0, то после возведения в квадрат имеем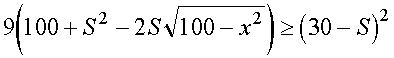 ,
,
![]() .
.
Квадратное неравенство относительно
S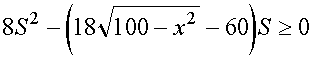
можно переписать в виде
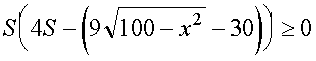 .
.
|
Для того, чтобы неравенство выполнялось при всех |
|
необходимо и достаточно, чтобы |
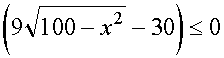 ,
,
|
откуда |
|
|
|
|
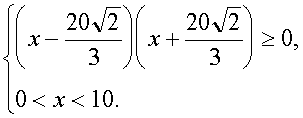
Методом интервалов находим
|
|
|
||
|
Таким образом , минимальное расстояние от A до дороги равно |
|
||
|
Ответ: |
|
. |