Пример
4.5.2. Путь из села в город идет сначала по грунтовой дороге, а затем по шоссе. Из села в город в 6 часов утра выехал мотоциклист. Одновременно с ним из города в село выехал автомобилист. Мотоциклист двигался по шоссе быстрее чем по грунтовой дороге в 3/2 раза, а автомобилист – в 8/3 раза (движение обоих по шоссе и по грунтовой дороге считается равномерным). Они встретились в 10 часов 30 минут, мотоциклист приехал в город в 14 часов, а автомобилист в село в 16 часов 30 минут. Определить, сможет ли мотоциклист приехать в город до 14 часов 30 минут, если он весь путь из села в город будет ехать с первоначальной скоростью?
Решение:
Пусть V1 – скорость мотоциклиста, а V2 – скорость автомобилиста при движении по грунтовой дороге, тогда 3V1/2 и 5V2/3 их скорости при движении по шоссе. Пусть S1 – длина грунтовой дороги, а S2 –
|
длина шоссе. Тогда на путь от села до города мотоциклист потратил |
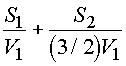
|
часов, что по |
|
условию равно 8 часов, а автомобилист |
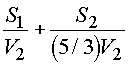
|
часов, что по условию равно 10,5 часов. |
|
В задаче требуется узнать, сможет ли мотоциклист менее чем за 8,5 часов проделать путь от села до |
|
города, т.е. выполняется ли неравенство |
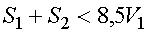
|
? |
Рассмотрим теперь два случая:
1) Предположим, что автомобилист и мотоциклист встретились на грунтовой дороге.

Тогда ясно, что мотоциклист за 4,5 часа проехал
4,5V1 км, а автомобилист проехал шоссейный участок дороги, а затем S1 - 4,5V1 км по грунтовке, затратив
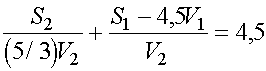 часов.
часов.
|
При этом ясно, что |
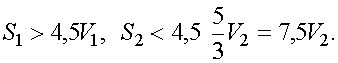
|
Таким образом, приходим к системе |
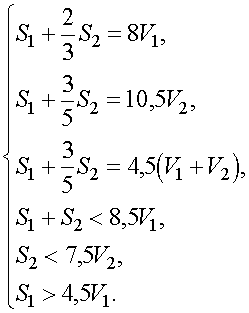
Из второго и третьего уравнений системы следует, что
V1 = 4V2/3. Далее, вычитая второе уравнение из первого и учитывая полученное соотношение, получаем
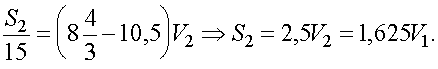
Однако, выражая из первого уравнения
S1 и подставляя его в третье неравенство системы, видим, что S2 должно удовлетворять неравенству S2 < 1,5V1, что противоречит, установленному выше соотношению 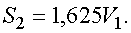
Итак, если бы точка встречи находилась на грунтовом участке дороги, то мотоциклист не смог бы весь путь проехать с первоначальной скоростью за 8,5 часов.
2) Пусть теперь точка встречи находится на шоссе.
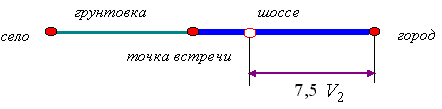
Тогда, как и в предыдущем пункте, получаем систему уравнений
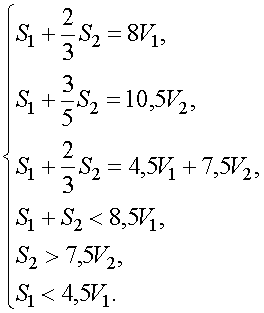
Вычитая из первого уравнения третье, получаем
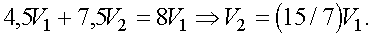
Теперь из первого и второго уравнения, учитывая полученное соотношение между скоростями, вытекает
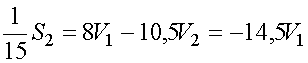 .
.
Таким образом, предположение, что точка встречи находится на шоссе, приводит к противоречию.
Ответ: нет.
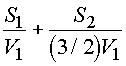
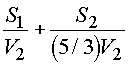
![]()

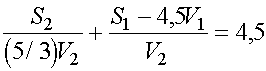 часов.
часов.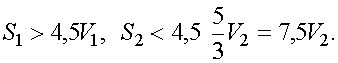
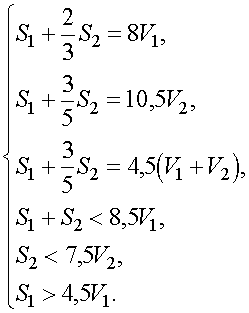
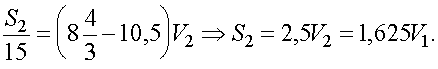

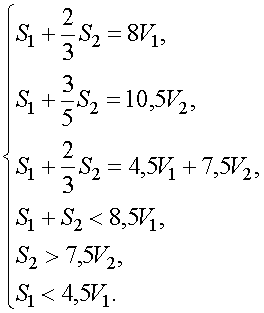
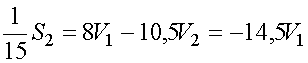 .
.