Пример
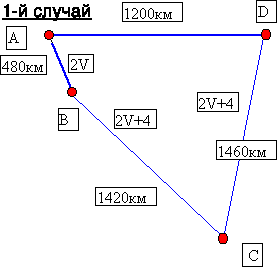
4.1.8. Парусник и пароход одновременно вышли из порта А и должны прибыть в порт D. Парусник, двигаясь с постоянной скоростью, прибыл в порт D, пройдя путь 1200 км. Пароход заходил в порты В и С, причём до порта В, расположенного от порта А на расстоянии 480 км, он плыл со скоростью, вдвое большей скорости парусника. Затем он увеличил свою скорость на 4 км/ч и прошел путь между портами В и С, равный 1420 км, и далее путь между портами С и D, равный 1460 км. На стоянке в портах С и В он затратил 1 сутки. В порт D пароход прибыл на двое суток позднее парусника. Если бы пароход плыл из порта А до порта В с той же скоростью, что и из порта В до порта D, то он прибыл бы в порт D на 1 сутки 20 ч позднее парусника. Найти скорость парусника.Решение: Пусть
V скорость парусника. Тогда на участке от А до В пароход имеет скорость 2V, а на участке ВС равна 2V +4.|
|
|
|
Условия задачи |
Уравнения |
|
Парусник, двигаясь с постоянно скоростью, прибыл в порт D, пройдя путь 1200 км. Пароход заходил в порты В и С, причём до порта В, расположенного от порта А на расстоянии 480 км, он плыл со скоростью, вдвое большей скорости парусника. Затем он увеличил свою скорость на 4 км/ч и прошел путь между портами В и С, равный 1420 км, и далее путь между портами С и D, равный 1460 км. На стоянке в портах С и В он затратил 1 сутки. В порт D пароход прибыл на двое суток позднее парусника. |
|
|
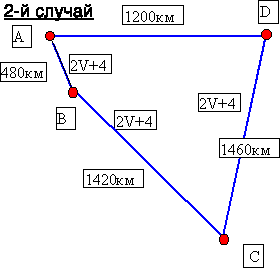
Если бы пароход плыл из порта А до порта В с той же скоростью, что и из порта В до порта D, то он прибыл бы в порт D на 1 сутки 20 ч позднее парусника. |
|
Итак, приходим к системе уравнений
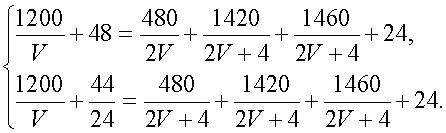
Заметим что мы должны определить переменное
V, удовлетворяющее обоим уравнениям|
системы. Вычтем из первого уравнения второе. Тогда получаем |
|
. |
|
Откуда после несложных преобразований с учетом неравенства |
|
получаем, что |
|
|
км/ч. |
Ответ: 10 км/ч.