В 12часов расположены следующим образом
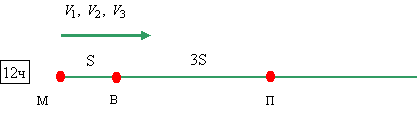
В 12ч 15 мин мотоциклист догнал велосипедиста.
![]()
В 12ч 40 мин мотоциклист догнал пешехода
![]()
Пусть
t время с начала движения, через которое велосипедист догнал пешехода. ![]()
Пример
4.1.6. (КубГУ, матем., 1990 г.) Мотоциклист, велосипедист и пешеход движутся по шоссе с постоянными скоростями в одну сторону. В 12 часов мотоциклист отставал от велосипедиста на расстояние в 3 раза меньшее, чем расстояние, на которое отставал велосипедист от пешехода. В 12 часов 15 минут мотоциклист догнал велосипедиста, а в 12 часов 40 минут – пешехода. Какое время будут показывать часы, когда велосипедист догонит пешехода?Решение:
1–й способ. Обозначим через V1, V2, V3 скорости мотоциклиста, велосипедиста и пешехода соответственно, а расстояние между мотоциклистом и велосипедистом в 12 часов дня через S.|
В 12часов расположены следующим образом |
|
||
|
В 12ч 15 мин мотоциклист догнал велосипедиста. |
|
||
|
В 12ч 40 мин мотоциклист догнал пешехода |
|
||
|
Пусть t время с начала движения, через которое велосипедист догнал пешехода. |
|
||
Таким образом, приходим к системе уравнений
|
Условия задачи |
Уравнения |
|
В 12 часов 15 минут мотоциклист догнал велосипедиста. |
|
|
В 12 часов 40 минут мотоциклист догнал пешехода. |
|
|
Через время t велосипедист догнал пешехода. |
|
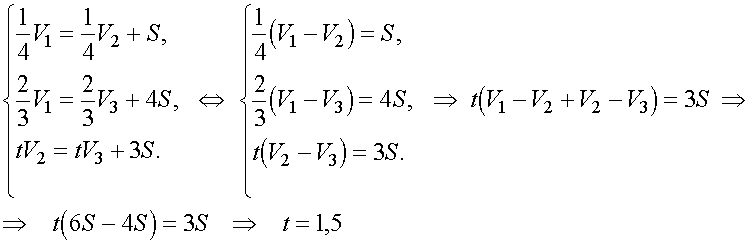
2–й способ
. Рассмотрим графическую модель задачи в системе координат: ось абсцисс – “время” t в часах, ось ординат – координата движения x(t). Так как движение равномерное, то графики зависимости координаты движения от времен для пешехода, велосипедиста и мотоциклиста являются прямыми с разными угловыми коэффициентами (в нашей интерпретации угловые коэффициенты и будут скоростями движения).|
OK – график движения мотоциклиста, AM – график движения велосипедиста, BM – график движения пешехода |
|
|
Заметим, что |
|
подобен |
|
, откуда |
|
(OS и SN – высоты |
|
|
). |
|
Однако |
|
, т.е. |
|
. |
|
Далее, |
|
подобен |
|
. Следовательно, |
|
|
Откуда, учитывая, что |
|
, |
|
, |
|
, |
получаем |
|||||||
|
|
, |
|
и тогда |
|
. |
|||||||||
Таким образом, в момент встречи часы показывали 13 часов 30 минут.![]()
Ответ: 13 часов 30 минут.