Условия задачи
Уравнения
Отправляясь из А в В, пешеход проходит участки АС (подъема) и СВ (спуска) за равные промежутки времени.
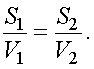
На обратном пути участок ВС пешеход проходит за промежуток времени в
k раз больший, чем время движения по участку СА.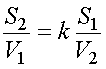 .
.
Пример
4.1.5. (КубГУ, матем., 1983 г.) Дорога между пунктами А и В проходит через перевал С. Отправляясь из А в В, пешеход проходит участки АС (подъема) и СВ (спуска) за равные промежутки времени. На обратном пути участок ВС пешеход проходит за промежуток времени вРешение:
Пусть скорость подъема V1 (км/ч), скорость спуска V2 (км/ч), S1 (км) – расстояние АС, S2 (км) – расстояние СВ. Тогда|
Условия задачи |
Уравнения |
|
Отправляясь из А в В, пешеход проходит участки АС (подъема) и СВ (спуска) за равные промежутки времени. |
|
|
На обратном пути участок ВС пешеход проходит за промежуток времени в k раз больший, чем время движения по участку СА. |
|
Следовательно, приходим к системе
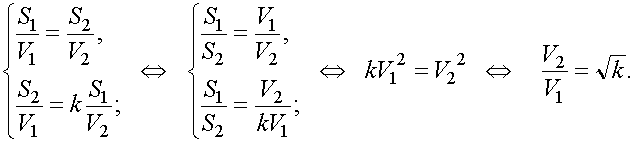
|
Ответ: отношение скоростей на спуске и на подъеме равно |
|
. |