момент встречи

Пример
4.1.4. (КубГУ, матем., 1986 г.) Из пунктов А и В выехали одновременно навстречу друг другу мотоциклист и велосипедист. Они встретились на расстоянии 4 км от В, а в момент прибытия мотоциклиста в В велосипедист находился в 15 км от А. Определить расстояние от А до В (скорость мотоциклиста больше скорости велосипедиста и эти скорости постоянны).Решение:
1–й способ. Пусть S – расстояние от А до В, а скорости мотоциклиста и велосипедиста V1 и V2 соответственно. К моменту встречи мотоциклист проехал (S – 4) км. Тогда получаем уравнение:|
момент встречи |
|
|
Условие задачи |
Уравнения |
|
Они встретились на расстоянии 4 км от В. |
|
|
Момент прибытия мотоциклиста в B |
|
|
Условие задачи |
Уравнение |
|
В момент прибытия мотоциклиста в В велосипедист находился в 15 км от А. |
|
Таким образом, приходим к системе уравнений
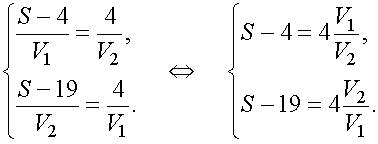
|
Откуда легко следует, что |
|
Последнее уравнение имеет два решения |
|||
|
|
и |
|
. Но второе решение не подходит по смыслу задачи, т.е. |
||
|
|
км. |
||||
2–й способ
. Простая и полезная модель задачи задается графиками равномерного движения в системе координат “время” (t – в часах) по оси абсцисс, “перемещение” (x – в км) по оси ординат.
|
|
Пусть AD–график движения мотоциклиста, BF– график движения велосипедиста, Е – точка встречи. Тогда ВС=4, AH – время, за которое мотоциклист прибыл в В, следовательно, FH=15. |
|
Заметим, что |
|
подобен |
|
, следовательно, |
|
, а |
|
|||
|
подобен |
|
, откуда |
|
|||||||
|
Пусть |
|
, тогда |
|
, |
|
. Таким образом, приходим |
к уравнению
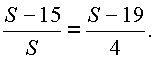
|
Решая полученное уравнение, находим корни |
|
Учитывая, что |
|
, |
приходим к ответу.
|
Ответ: |
|
км. |