Условия задачи
Уравнения
Если бы первый самолет вылетел на
20 минут позже второго, то они встретились бы на четверти пути от А.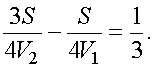
Если бы второй самолет вылетел на
20 минут позже первого, то они встретились бы на полпути.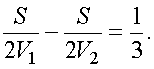
Пример
4.1.2. (КубГУ, матем., 1972 г.)Два самолета вылетели одновременно из пунктов
A и B навстречу друг другу и встретились на расстоянии 100 км от середины AB. Если бы первый самолет вылетел на 20 минут позже второго, то они встретились бы на четверти пути от A, а если бы второй самолет вылетел на 20 минут позже первого, то они встретились бы на полпути. Определить скорости самолетов.Решение:
Пусть скорости первого и второго самолетов равны соответственно V1 и V2 км/ч, а расстояние между A и В – S км.Для составления системы уравнений составим таблицу:
|
Условия задачи |
Уравнения |
|
Если бы первый самолет вылетел на 20 минут позже второго, то они встретились бы на четверти пути от А. |
|
|
Если бы второй самолет вылетел на 20 минут позже первого, то они встретились бы на полпути. |
|
Заметим, что как видно из второго уравнения V
2 > V1 т.е. первое условие задачи позволяет заключить:|
Самолеты встретились на расстоянии 100 км от середины |
|
Таким образом, приходим к системе уравнений
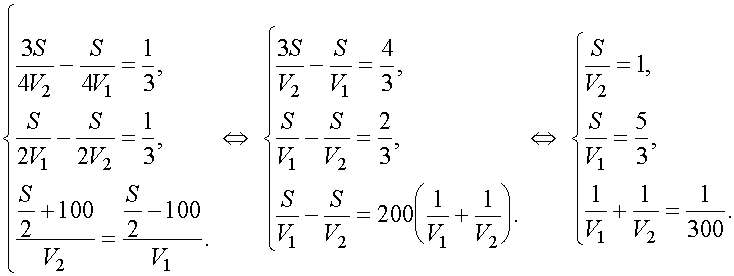
|
Откуда S = 800 км, |
|
км/ч, |
|
км/ч. |