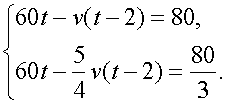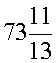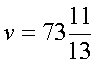Решение: Пусть скорость мотоциклиста v км/ч, а t – время до момента, когда расстояние
между ними впервые стало равно
80 км. Тогда за время t ч грузовик прошел расстояние60t
км, а мотоциклист за время t - 2 проехал v(t - 2) км. Откуда получаем уравнение![]()
.
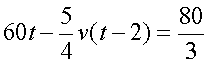 .
.