Пример 1
. Решить систему уравнений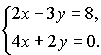
|
Пример 1 . Решить систему уравнений |
|
Решение
: Рассмотрим три способа решения этой системы.а) Выразим из любого уравнения одно из неизвестных, например, y, из второго уравнения y= - 2x и подставим его в первое уравнение:
2x-3(-2x)= 8 или 8x= 8, откуда получаем x= 1. А значение второго неизвестного получим из соотношения y= -2x, т.е. y= -2.
Ответ: (1;-2).
b) Умножая обе части первого уравнения на (-2) и складывая его со вторым уравнением, получим следующее уравнение
(-4x+4x)+(6y+2y)= -16 или 8y= -16, т.е. y= -2.
Другое неизвестное можно найти из любого уравнения исходной системы, подставив в него значение
y= -2.
Ответ: (1;-2).
Мы применили метод алгебраического сложения двух уравнений с целью избавления от одного из неизвестных, предварительно умножив одно из уравнений на подходящий множитель (в силу этих соображений иногда этот метод называют методом “выравнивания коэффициентов” при одном из неизвестных с дальнейшим вычитанием одного уравнения из другого).
с) Решим эту систему с помощью определителей. Вычислим эти определители
|
|
|
|
|
|
||
|
Тогда |
|
|
Ответ: (1;-2).
Рассмотрим еще один метод решения линейных систем – метод последовательного исключения неизвестных (метод Гаусса), приводящий систему уравнений к треугольному (трапецеидальному) виду. Этот метод успешно может быть применен к решению линейных систем с любым числом уравнений и неизвестных.
|
Пример 2. Решить систему уравнений |
|
Решение
: Решаем эту систему методом Гаусса. Привести эту систему к треугольному (трапецеидальному) виду означает, что во втором уравнении не должно быть первого неизвестного (или иметь при нем нулевой коэффициент), а в третьем – первого и второго неизвестного. Тогда из последнего уравнения находится третье неизвестное, а подставляя его значение во второе уравнение системы, найдем второе неизвестное. Первое неизвестное находится из первого уравнения системы, куда предварительно подставлены найденные значения двух других.Сначала умножим первое уравнение системы на (-2) и сложим его со вторым уравнением, а к третьему уравнению добавим первое, умноженное на (-3), в результате чего получим систему
|
|
Теперь умножим второе уравнение на 5, а третье – на (-7) (уравниваем коэффициенты при неизвестном y) и сложим после этого последние два уравнения (первое и второе уравнение переписываем, а на месте третьего уравнения запишем результат сложения уравнений с выровненными коэффициентами при неизвестном y).
|
|
Из последнего уравнения находим z=2, подставим его во второе уравнение системы и найдем y= -2. Подставляя эти значения неизвестных в первое уравнение, находим x= 1.
Ответ: (1;-2;2).
|
Пример 3 . Решить систему уравнений |
|
Решение
: Приведем эту систему к треугольному (трапецеидальному) виду|
|
или |
|
Мы получили систему из двух уравнений с тремя неизвестными. В этом случае одно из двух неизвестных второго уравнения выражают через другое (“свободное” неизвестное) и подставляют в первое уравнение, из которого выражают первое неизвестное через это же “свободное” неизвестное.
Пусть во втором уравнении “свободным” неизвестным будет z.
|
Тогда |
|
а первое уравнение перепишем при этом |
|
|
условии и найдем выражение для x: |
|
||
Решения исходной системы (бесконечное множество) могут быть записаны в этом случае так
|
|
|
z= k, где k – любое действительное число. |
Например, при k= -5 получим x= 5, а y= 3; а при k= 2 получаем следующий набор чисел (1;-2;2) и т.д.
|
Ответ: |
|
|
|
Пример 4 . Решить систему уравнений |
|
Решение
: Как и в предыдущих примерах, приведем эту систему к треугольному (трапецеидальному) виду|
|
Очевидно, что последние два уравнения противоречивы, а тогда система – несовместна ( не имеет решений).
Ответ: система не имеет решения.