Содержание раздел Разобранные примеры Задачи для самостоятельного решения

Пример 6. Решить неравенство

. (6)

Решение

Приравнивая к нулю коэффициент при , находим первое контрольное значение параметра a=0. Вычислим дискриминант квадратного трехчлена 
 

.
 

Приравнивая к нулю найденный дискриминант, найдем второе контрольное значение a=-1. Неравенство (6) будем решать в каждом из следующих случаев:

1) a<-1; 2) a=-1; 3) -1<a<0; 4) a=0; 5) a>0.

1) Если a<-1, то трехчлен  имеет корни 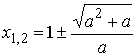, причем .

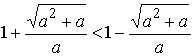Так как при этом ветви параболы  направлены вниз, то решением неравенства (6) будет

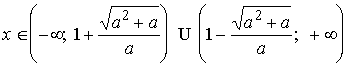. 2) Если a=-1, то получаем неравенство , решением которого будет .
3) Если -1<a<0, то дискриминант и коэффициент при  будут отрицательными. Значит трехчлен  будет отрицателен при всех x, т.е. решением неравенства (6) будут .
4) Если a=0, то неравенство (6) принимает вид -1<0, т.е. верно при любом .

5) Если a>0, то имеем 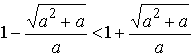 и ветви параболы направлены вверх, следовательно, решением неравенства (6) будут
 

.

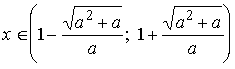Учитывая возможность объединения записи ответа в случаях 1) и 2), а также 3) и 4), получим ответ.

Ответ: 1) если , то

;

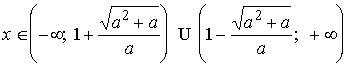          2) если , то ;

          3) если , то .
 

Содержание раздела Разобранные примеры Задачи для самостоятельного решения