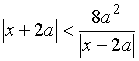Содержание раздела Разобранные примеры Задачи для самостоятельного решения

Пример 15. Для всех значений параметра a решить неравенство

.

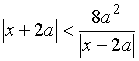Решение

Так как  для всех , то имеем
 

или .

Это неравенство равносильно системе неравенств

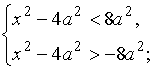
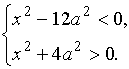
Второе неравенство верно при всех x. Решая первое неравенство методом интервалов с учетом того, что , получим

а) при a>0 

б) при a<0 
 

в) при a=0  решений не имеет.

Ответ: при a>0 ;

           при a<0 ;

           при a=0 решений нет.
 

Содержание раздела Разобранные примеры Задачи для самостоятельного решения