![]() Содержание
раздела
Содержание
раздела![]() Разобранные
примеры
Разобранные
примеры![]() Задачи
для самостоятельного решения
Задачи
для самостоятельного решения
Утверждение1
Утверждение2
Утверждение3
Утверждение4
Утверждение5
Утверждение6
Утверждение7
Пусть f(x)=ax2+bx+c
имеет действительные корни x1
и x2, а M – какое-нибудь
действительное число, D=b2 -4ас
Утверждение 1. Для того чтобы оба корня квадратного трехчлена были меньше, чем число M (т.е. лежали на числовой оси левее, чем точка M), необходимо и достаточно выполнение следующих условий:
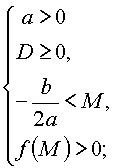 |
или | 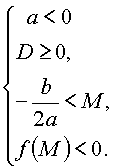 |
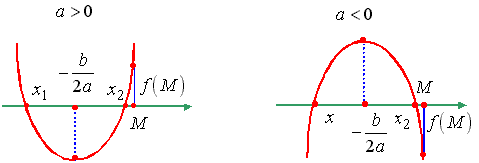
Утверждение 2. Для того чтобы один из корней квадратного трехчлена был меньше, чем число M, а другой больше, чем число M (т.е. точка M лежала бы между корнями), необходимо и достаточно выполнение условий:
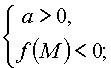 |
или | 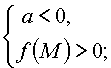 |
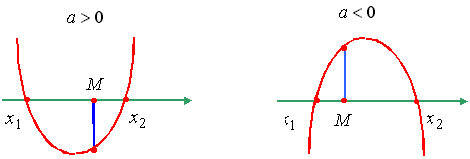
Утверждение 3. Для того чтобы оба корня квадратного трехчлена были больше, чем число M (т.е. лежали на числовой оси правее, чем точка M), необходимо и достаточно выполнение условий:
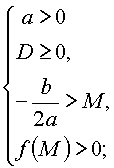 |
или | 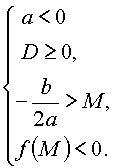 |
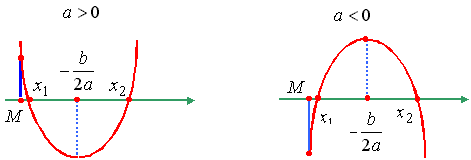
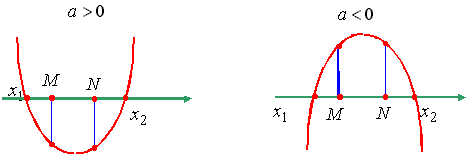
Утверждение 4. Для того чтобы оба корня квадратного трехчлена были больше, чем число M, но меньше, чем число N (M<N), т.е. лежали в интервале между M и N, необходимо и достаточно:
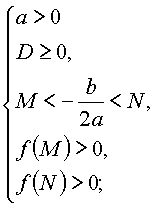 |
или | 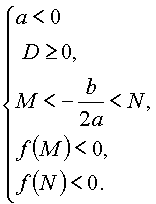 |
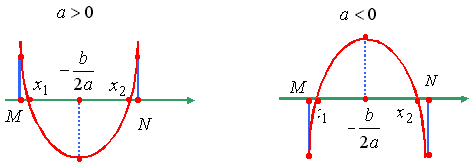
Утверждение
5. Для того чтобы только больший корень квадратного трехчлена
лежал в интервале [M,N] (M < N), необходимо и достаточно:
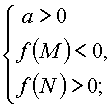 |
или | 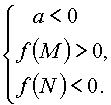 |
(при этом меньший корень
лежит вне отрезка [M, N]).
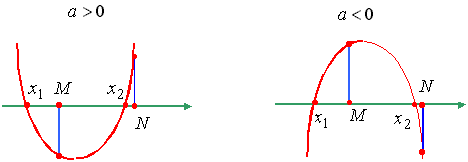
Утверждение 6. Для того чтобы только меньший корень квадратного трехчлена лежал в интервале [M, N], необходимо и достаточно:
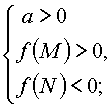 |
или | 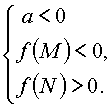 |
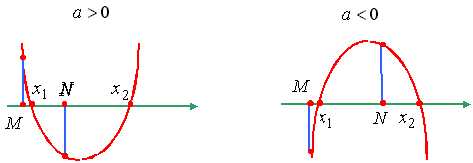
Утверждение
7. Для того чтобы
один из корней квадратного трехчлена был меньше, чем M, а другой больше,
чем N (M < N), т.е. отрезок [M, N] целиком лежал внутри интервала между
корнями, необходимо и достаточно:
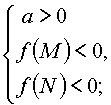 |
или | 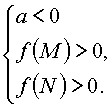 |
![]() Содержание
раздела
Содержание
раздела![]() Разобранные
примеры
Разобранные
примеры![]() Задачи
для самостоятельного решения
Задачи
для самостоятельного решения