Итоговые таблицы исследования тригонометрических функций и их графики
|
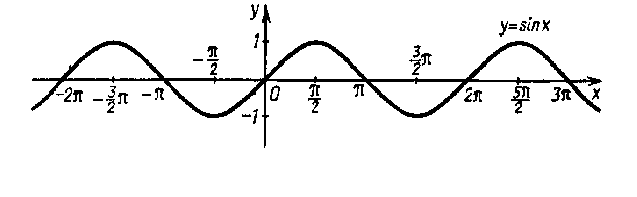
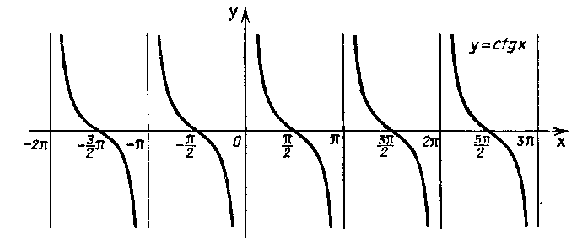Монотонность, производные тригонометрических функций
|
Зная производные тригонометрических функций
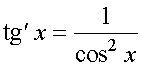
и условие возрастания (на промежутках, где производная функции положительна) и убывания ( на промежутках, где производная функции отрицательна) функций, составим следующую наглядную таблицу: |
|
y = sinx |
0; p/2 |
p/2 |
p/2; p |
p |
p; 3p/2 |
3p/2 |
3p/2;2p |
2p |
|
|
|
m a x |
|
п е р е г и б |
|
m i n |
|
п е р е г и б |
График функции
y = sinx имеет вид:
|
y = cosx |
0; p/2 |
p/2 |
p/2; p |
p |
p; 3p/2 |
3p/2 |
3p/2;2p |
2p |
|
|
|
п е р е г и б |
|
m i n |
|
п е р е г и б |
|
m a x |
График функции
y = cosx имеет вид:
|
y = tgx |
-p/2; p/2 |
0 |
0 p/2 |
p /2 |
p /2; p |
p |
p;3p/2 |
3p/2 |
|
|
|
п е р е г и б |
|
Р А З Р Ы В |
|
п е р е г и б |
|
Р А З Р Ы В |
График функции
y = tgx имеет вид:
График функции
y = ctgx имеет вид:
