ПРОИЗВОДНАЯ ФУНКЦИИ

ПРОИЗВОДНАЯ ФУНКЦИИ

Рассмотрим произвольную внутреннюю точку x₀ области определения функции y = f(x).

Разность

где x - также внутренняя точка области определения, называется

приращением аргумента в точке x₀. Разность

называется

приращением функции в точке x₀, соответствующим приращению

и обозначается

Производной функции y = f(x) в точке x₀ называется предел отношения приращения

функции к приращению аргумента в этой точке при стремлении приращения аргумента к нулю, если такой предел существует и конечен, т.е.

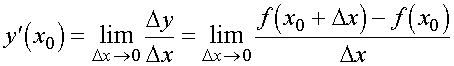
ОСНОВНЫЕ СВОЙСТВА ПРОИЗВОДНЫХ

Если в точке x существуют конечные производные функций v = v(x) и u = u(x),

то в этой точке существуют также производные суммы, разности, произведения и частного этих функций, причем:

1.
2.
3.
4.	(при	);
5.

1. Производная сложной функции

Если функция y = f(x) имеет производную в точке x₀, а функция y = g(x) имеет производную

в точке y₀ = f(x₀), то сложная функция h(x) = g(f(x))

также имеет производную в точке x₀, причем

2. Достаточное условие монотонности функции

Если в каждой точке интервала (a; b) выполнено неравенство

то функция y = f(x) возрастает на этом интервале.

Если

при

то y = f(x) убывает на (a; b).

3. Необходимое условие экстремума функции

Если точка x₀ является точкой экстремума функции y = f(x) и в этой точке

существует производная

то она равна нулю

4. Признак максимума функции

Если функция y = f(x) определена на интервале (a; b), непрерывна в точке

имеет производную

на интервалах

на интервале

то точка

x₀ является точкой максимума функции

5. Признак минимума функции

Если функция

определена на интервале

непрерывна в

точке

имеет производную

на интервалах

на интервале

то точка x₀ является точкой минимума функции

Правило отыскания наибольшего и наименьшего значений функции.

Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек (точек из области определения, в которых производная функции обращается в ноль или не существует), нужно вычислить значения функции во всех критических точках и на концах отрезка и выбрать наибольшее и наименьшее из полученных чисел.