Пример
3.1.6. (КубГУ, эконом., 1986 г.)Решить неравенство
![]() .
.
Решение:
|
ОДЗ неравенства определяется неравенством |
|
|
решение которого, как и в 1-м способе, легко находится методом интервалов: |
|
|
|
|
|
Далее, найдем интервалы знакопостоянства функции |
|
|
|
Для этого решим уравнение |
![]()
Имеем, возводя обе части в квадрат и преобразовывая полученные выражения:
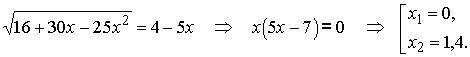
|
Подстановкой убеждаемся, что решением уравнения является только x1 = 0. |
|||||||
|
Следовательно, в ОДЗ f(x) имеет два промежутка знакопостоянства |
|
||||||
|
и |
|
причем т.к. |
|
а |
|
распределение |
|
знаков определяется следующим образом

|
Таким образом, получаем множество решений неравенства: |
|