6.10.1. Стороны AD и BC равнобедренной трапеции ABCD параллельны. Высота трапеции равна h. Сторона AB из центра описанной окружности видна под углом 120°. Найти площадь трапеции.

    Ответ: .

    6.10.2. В квадрат вписана окружность, в окружность вписан правильный треугольник, в треугольник вновь вписана окружность, в получившуюся окружность вписан квадрат. Во сколько раз площадь последнего квадрата меньше площади исходного квадрата?

    Ответ: в 8 раз.

    6.10.3. На основании AC треугольника ABC, как на диаметре, построена окружность, которая пересекает стороны AB и BC в точках M и N соответственно. Найти радиус окружности, если AB = a  и  ИAM = a, ИCN = b.

    Ответ: .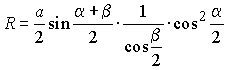

    6.10.4. В равнобедренном треугольнике 30° с основанием AB угол , а длина высоты на основание равна 17. В угол C вписана окружность, которая касается стороны BC  в точке M и отсекает от основания отрезок KE. Найти площадь DKME, если длина CM = 8.

    Ответ: .

    6.10.5. В равнобедренном треугольнике ABC с основанием AB  угол A равен углу B и равен . Окружность, вписанная в угол C, касается стороны BC в точке M и отсекает от основания отрезок EK. Найти площадь DKME, если центр окружности удален от C на расстояние  и длина .

    Ответ: .

    6.10.6. Около окружности радиуса R описан параллелограмм. Площадь четырехугольника с вершинами в точках касания окружности и параллелограмма равна S. Найти стороны параллелограмма.

    Ответ: .

    6.10.7. Общая касательная к двум пересекающимся окружностям радиусов R и r (А и В точки касания) пересекает продолжение их общей хорды MN в точке D (N между D и M). Найти: 1) радиус окружности, описанной около треугольника AMB; 2) отношение высот треугольников AMD и DMB, опущенных из вершины D.

    Ответ: , .

    6.10.8. Стороны AD и BC трапеции ABCD параллельны, причем AD = 3, а угол С равен 120°. Прямые BC и CD являются касательными к окружности, описанной около треугольника ABD. Найти площадь треугольника ABD.

    Ответ:  .

    6.10.9. Окружность, построенная на стороне АС треугольника АВС, как на диаметре, проходит через середину стороны ВС и пересекает сторону АВ в точке D так, что . Найти площадь треугольника АВС, если AC = 1.

    Ответ: .

    6.10.10. В треугольнике АВС известна сторона AB = 4, РBAC = 30°, РABC = 130°. На АВ, как на диаметре, построен круг. Найти площадь круга внутри треугольника.

    Ответ: .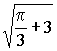

    6.10.11. Основание АС равнобедренного треугольника АВС является хордой окружности, центр которой лежит внутри треугольника АВС. Прямые, проходящие через точку В, касаются окружности в точках D и E. Найти площадь треугольника DBE, если AB = BC = 2, , а радиус окружности равен 1.

    Ответ: .

    6.10.12. На продолжении стороны AD ромба ABCD за точку D взята точка К. Прямые АС и ВК пересекаются в точке М. Известно, что AK = 14 и что точки А, В и М лежат на окружности радиуса 6, центр которой принадлежит отрезку АК. Найти длину отрезка ВК.

    Ответ: 7.

    6.10.13. Выпуклый четырехугольник ABCD вписан в окружность. Диагональ AC является биссектрисой угла BAD и пересекается с диагональю BD в точке K. Найти длину отрезка KC, если длина отрезка BC равна 4, а длина отрезка AK равна 6.
 
    Ответ: 2.

    6.10.14. Отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, равны 4 см и 6 см. Площадь четырехугольника равна 16 см. Найти диагонали.

    Ответ: 6, .

    6.10.15. В параллелограмме со сторонами a и b и острым углом  a  найти тангенсы  углов,  образуемых  большей диагональю параллелограмма с его сторонами.
    Ответ: .
    6.10.16. Дана  трапеция, в которую можно вписать окружность. Известно, что она равносторонняя  с боковой стороной, равной  12 см, и площадью, равной 48  см. Найти ее основания.
    Ответ: .
    6.10.17.  Дан квадрат, сторона которого равна a. Определить стороны равновеликого ему равнобедренного треугольника, у которого сумма длин оснований и высоты равна сумме длин двух боковых сторон    .
    Ответ: .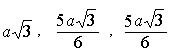
    6.10.18.  Точки M, N, P  и K являются серединами сторон AB, BC, CD, DA  ромба ABCD. Вычислить площадь фигуры, являющейся пересечением четырехугольников ABCD, ANCK, BPDM, если площадь ромба равна 100 см .
    Ответ:  20 см .

    6.10.19.  В окружность вписан четырехугольник с углами  120°,  90°, 60° , 90° . Площадь четырехугольника равна  см. Найти радиус окружности, если диагонали четырехугольника взаимно перпендикулярны.
    Ответ 3 см.

    6.10.20. Найти площадь трапеции, у которой боковые стороны и меньшее основание равны, высота равна h  и тупой угол равен a.
    Ответ: .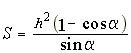

    6.10.21. Непараллельные стороны трапеции продолжены до взаимного пересечения, и через полученную точку проведена прямая, параллельная основаниям трапеции. Найти отрезок этой прямой, ограниченный продолженными диагоналями, если основания трапеции  a  и b, a  > b  .
    Ответ: .

    6.10.22. Центр окружности, касающейся стороны  BC треугольника ABC  в точке B  и проходящей через  A, лежит на отрезке  AC. Найти площадь треугольника  ABC, если известно, что  BC = 6 см,  AC = 9 см.
    Ответ:  S = 135/13 см .

    6.10.23.  Прямая делит длину дуги окружности в отношении 1 : 3.   В каком отношении она делит площадь круга?
    Ответ: .

    6.10.24. В равнобедренной трапеции основания равны  a  и b, угол диагонали с основанием равен  a. Найти длину отрезка, соединяющего точку пересечения диагоналей с серединой боковой стороны трапеции.
    Ответ: .

    6.10.25. Центр полуокружности, вписанной в прямоугольный треугольник так, что её диаметр лежит на гипотенузе, делит гипотенузу на отрезки 3 и 4. Найти длину дуги полуокружности, заключенной между точками касания с катетами.
    Ответ:  1,2 p .

    6.10.26.  Один из катетов прямоугольного треугольника равен 15 см, а проекция другого катета на гипотенузу равна 16 см. Найти радиус окружности, вписанной в треугольник.
    Ответ:  r =  5 см.

    6.10.27. Радиус окружности, описанной около прямоугольного треугольника, равен 5 см, а радиус окружности, вписанной в этот треугольник, равен 2 см. Найти периметр этого треугольника.
    Ответ:  24 см.

    6.10.28. Вычислить  площадь равнобедренной трапеции по разности оснований, равной 14 см, и боковой стороне, равной 16 см,  если известно, что в трапецию можно вписать окружность.
    Ответ: .

    6.10.29. Доказать, что для произвольного треугольника выполняется равенство 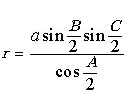,  где r – радиус вписанной окружности; A, B, C  – углы треугольника; a = BC.

    6.10.30. Доказать справедливость следующих формул для площади треугольника: , , где A, B, C  – углы треугольника; a – сторона, лежащая против угла  A; R  – радиус описанной окружности.