ЗАОЧНАЯ МАТЕМАТИЧЕСКАЯ ШКОЛА
1998 - 1999 уч.г.
10 класс, 1 часть.
Задания для самостоятельного решения
.
Составитель: доцент кафедры теории функций КубГУ Тлюстен С.Р.
методист ЦДО Шелег Т.А.
Через каждую вершину выпуклого четырехугольника ABCD проведена прямая, параллельная его диагонали (рис. 1). Докажите, что площадь полученного параллелограмма EFGH в два раза больше площади ABCD.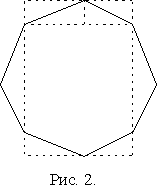 Доказать, что площадь правильного восьмиугольника равна произведению длин самой короткой и самой длинной из его диагоналей. (Указание: посмотрите на рисунок 2).
В трапеции ABCD (BC || AD) точка К - середина АВ - соединена отрезками с вершинами С и D. Найти отношение площади треугольника KCD к площади ABCD.
Доказать, что диагональ четырехугольника делит его площадь пополам тогда и только тогда (см. замечание к примеру 3), когда она делит пополам другую его диагональ.
Доказать, что выпуклый четырехугольник является параллелограммом тогда и только тогда, когда каждая из его диагоналей делит его площадь пополам (можно использовать задачу 4, даже если Вы ее не решили).
Точка, лежащая внутри параллелограмма, соединена отрезками со всеми его вершинами. Доказать, что суммы площадей противолежащих треугольников, на которые разбивается параллелограмм, равны.
Доказать, что сумма расстояний от любой точки внутри правильного пятиугольника ABCDE до прямых AB, BC, CD, DE и ЕА одна и та же. (Указание: используйте идеи доказательства примера 4 из текста задания).
На стороне АВ треугольника АВС взяты очки D и Е так, что AD= DE=
Доказать, что площадь правильного восьмиугольника равна произведению длин самой короткой и самой длинной из его диагоналей. (Указание: посмотрите на рисунок 2).
В трапеции ABCD (BC || AD) точка К - середина АВ - соединена отрезками с вершинами С и D. Найти отношение площади треугольника KCD к площади ABCD.
Доказать, что диагональ четырехугольника делит его площадь пополам тогда и только тогда (см. замечание к примеру 3), когда она делит пополам другую его диагональ.
Доказать, что выпуклый четырехугольник является параллелограммом тогда и только тогда, когда каждая из его диагоналей делит его площадь пополам (можно использовать задачу 4, даже если Вы ее не решили).
Точка, лежащая внутри параллелограмма, соединена отрезками со всеми его вершинами. Доказать, что суммы площадей противолежащих треугольников, на которые разбивается параллелограмм, равны.
Доказать, что сумма расстояний от любой точки внутри правильного пятиугольника ABCDE до прямых AB, BC, CD, DE и ЕА одна и та же. (Указание: используйте идеи доказательства примера 4 из текста задания).
На стороне АВ треугольника АВС взяты очки D и Е так, что AD= DE= 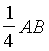 , BE=
, BE= 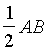 . На стороне ВС взяты точки F и G так, что BF= FG= GC=
. На стороне ВС взяты точки F и G так, что BF= FG= GC= 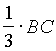 . А на стороне АС взяты точки К и L так, что СК= КL=
. А на стороне АС взяты точки К и L так, что СК= КL= 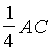 , LА=
, LА= 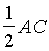 . Найти отношение площадей
. Найти отношение площадей 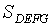 и
и 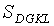 . (Указание: выразите эти площади через
. (Указание: выразите эти площади через 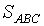 , используя свойство 5).
Пусть на стороне ВС треугольника АВС так выбраны точки К и L, что Р САК= Р ВАL. Доказать, что
, используя свойство 5).
Пусть на стороне ВС треугольника АВС так выбраны точки К и L, что Р САК= Р ВАL. Доказать, что 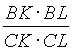 =
= 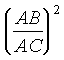 .
В трапеции ABCD (BC || AD) диагонали АС и ВD пересекаются в точке О. Известно, что
.
В трапеции ABCD (BC || AD) диагонали АС и ВD пересекаются в точке О. Известно, что 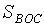 =a;
=a; 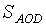 =b. Найти площадь трапеции ABCD. (Указание: используйте результат примера 3 из текста задания).
Две медианы треугольника перпендикулярны между собой. Их длины равны m и n. Чему равна площадь треугольника.
Дан треугольник АВС. На отрезке ВС выбрана точка D. Доказать, что радиус окружности, вписанной в треугольник ABC, меньше суммы радиусов окружностей, вписанных в треугольники ABD и ACD. (Указание: используйте формулу (3)).
Внутри треугольника АВС лежит точка М. Докажите, что площади треугольников ABM и CBM равны тогда и только тогда, когда М лежит на медиане к стороне АС. (Указание: пусть точка К лежит на пересечении прямой ВМ с АС. Используйте свойство 4).
=b. Найти площадь трапеции ABCD. (Указание: используйте результат примера 3 из текста задания).
Две медианы треугольника перпендикулярны между собой. Их длины равны m и n. Чему равна площадь треугольника.
Дан треугольник АВС. На отрезке ВС выбрана точка D. Доказать, что радиус окружности, вписанной в треугольник ABC, меньше суммы радиусов окружностей, вписанных в треугольники ABD и ACD. (Указание: используйте формулу (3)).
Внутри треугольника АВС лежит точка М. Докажите, что площади треугольников ABM и CBM равны тогда и только тогда, когда М лежит на медиане к стороне АС. (Указание: пусть точка К лежит на пересечении прямой ВМ с АС. Используйте свойство 4).
14*. В треугольнике АВС на сторонах АВ
, ВС и АС взяты точки К, L и М соответственно так, что 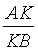 =
= 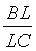 =
= 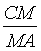 =
= 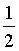 . Отрезок AL пересекается с отрезком ВМ в точке D, а с отрезком СК - в точке Е. Отрезки ВМ и СК пересекаются в точке F. Найти отношение
. Отрезок AL пересекается с отрезком ВМ в точке D, а с отрезком СК - в точке Е. Отрезки ВМ и СК пересекаются в точке F. Найти отношение 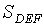 :
: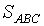 . (Указание: используйте теорему 1).
. (Указание: используйте теорему 1).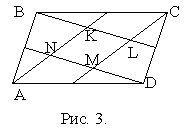
15*. На сторонах выпуклого четырехугольника
ABCD взяты точки M, P, K, H так, что 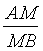 =
= 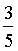 ;
; 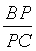 =
= 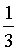 ;
; 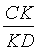 =
= 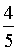 ;
; 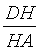 =
= 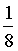 . Найти отношение площади шестиугольника MBPKDH к площади четырехугольника ABCD. (Указание: проведите диагональ BD и воспользуйтесь свойством 5).
. Найти отношение площади шестиугольника MBPKDH к площади четырехугольника ABCD. (Указание: проведите диагональ BD и воспользуйтесь свойством 5).
16*. Вершина А параллелограмма АВСD соединена отрезком с серединой стороны ВС, вершина В - с серединой СD, вершина С - с серединой
AD, вершина D - с серединой АВ. Пусть точки пересечения этих отрезков внутри АВСD - это точки K, L, M и N (см. рис. 3). Доказать, что KLMN - параллелограмм и 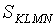 =
= 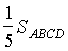 .
.
17*. Дан правильный треугольник АВС со стороной 2. Через середину М стороны АВ проведена прямая, пересекающая сторону АС в точке
N и продолжение стороны ВС (за точку С) в точке D. Площади треугольников АМN и NCD равны. Найти длину отрезка СN.
Задания, отмеченные звездочкой, - более трудные. Для получения отличной оценки необходимо решить хотя бы одну такую задачу.
Internet-School | Наши адреса | Правила оформления рукописей заданий | Методические указания


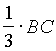 . А на стороне АС взяты точки К и L так, что СК= КL=
. А на стороне АС взяты точки К и L так, что СК= КL= 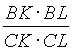 =
= 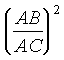 .
.

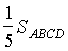 .
.