|
350088 г. Краснодар |
ЗАОЧНАЯ ШКОЛА |
Аналогично, ![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() .
.
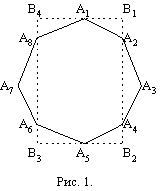
Поэтому ![]() =
= ![]() +
+ ![]() +
+
![]() +
+ ![]() = 2(
= 2(![]() +
+ ![]() +
+
![]() +
+ ![]() )
=
)
= ![]() .
.
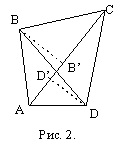
Допустим теперь, что ![]() =
=
![]() .
Из формулы (1) получаем, что тогда ВВ’ = DD’.
Теперь прямоугольные треугольники BOB’ и
DOD’ равны по катету и острому углу и,
следовательно, OB=OD.
.
Из формулы (1) получаем, что тогда ВВ’ = DD’.
Теперь прямоугольные треугольники BOB’ и
DOD’ равны по катету и острому углу и,
следовательно, OB=OD.
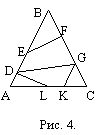
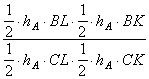 =
= 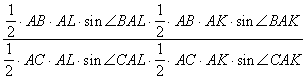 =
=
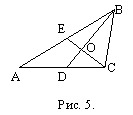
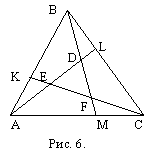
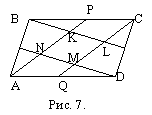
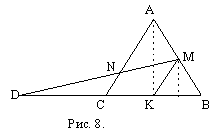
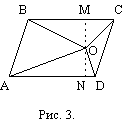
Очевидно, МК ||
АС (МК
- средняя линия АВС), МК=1,
СК=1, СD=
BD-BC= 2. Из подобия треугольников
DNC и DMK
получаем: ![]() =
=
![]() и СN=
и СN= ![]() =
=
![]() =
= ![]() .
.
Замечание: После того, как мы доказали, что BD=4, можно было применить теорему 1.