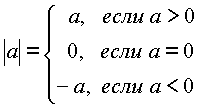
8 класс

Методические рекомендации

Составитель: Подберезкина А.И., преподаватель кафедры теории функции.

1 часть

Перед тем, как приступить к решению задач из раздела 2, следует внимательно ознакомится с разделом 1, где приведены теоретические сведения и разобраны примеры решения задач.

Рассмотрим вначале понятие абсолютной величины действительного числа.

Определение. Абсолютной величиной (модулем) действительного числа а называется само число а, если оно неотрицательное, и число противоположное а, если а отрицательное.

Абсолютную величину числа а обозначают |а| и читают “модуль а ”.

Из определения абсолютной величины числа следует:

Примеры:

т.к.

т.к.

Отметим некоторые

свойства абсолютной величины.

  1. Противоположные числа имеют равные модули, т.е.

В самом

деле, по определению имеем:

Следовательно,

2.

(теорема верна для любого конечного числа

сомножителей). Докажем это свойство. Рассмотрим все случаи:

1) Если а=0 и b=0 или а=0, но

или

но b=0 ,

то очевидно, что

2)Если а > 0 и b > 0 тогда а=|a| , b=|b| и ab > 0. Значит, |ab|=ab=|a||b|.

3)Если а < 0 и b < 0, тогда -а=|a|, -b=|b| и ab > 0. Значит, |ab|=ab=(-a)

(-b)=|a| |b|.

4) Если a > 0 и b < 0, тогда a=|a|, -b=|b| и ab < 0. Значит,

|ab|=-ab=a (-b)=|a| |b|, и свойство 2 доказано.

3.

где

Попытайтесь доказать самостоятельно!

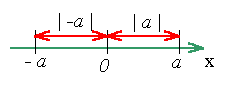
Известно, что каждому действительному числу можно поставить в соответствие точку числовой прямой, тогда эта точка будет геометрическим изображением данного действительного числа. Каждой точке числовой прямой соответствует ее расстояние от начала отсчета, или длина отрезка, начало которого в точке начала отсчета, а конец - в данной точке. Это расстояние, или длина отрезка рассматривается всегда как величина неотрицательная. Таким образом, геометрической интерпретацией модуля действительного числа а будет расстояние от начала отсчета до точки, изображающей число.

Геометрическое толкование смысла |a| наглядно подтверждает, что |-a|=|a|.

Отсюда легко понять, что

|x-a|=|a-x|.

Пример 2. а) Если |a|=5, то а1= 5 и а2=-5 или

Следовательно,

данному равенству удовлетворяют два числа, которым на числовой прямой соответствуют 2 точки;

б) Если |x|=b, где необходимо

то

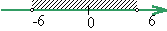
в) Если |x|=b, то

г) Если |a|<6; то а<6, если

т.е.

a<6 или a>-6, если a<0, - т.е. -6<a<0,

откуда -6<a<6. Следовательно, неравенству |a|<6 удовлетворяет множество точек промежутка (-6; 6) числовой прямой;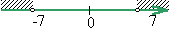

д) Если |a|>7, то a>7, если a>0, или -a>7, если a<0, т.е. a<-7. Откуда , a>7 и a<-7. Следовательно, неравенству |a|>7 удовлетворяют два промежутка

числовой оси:

и

Рассмотрим теперь примеры решения уравнений и системы уравнений, содержащих абсолютные величины. Их можно разбить условно на следующие группы:

1) Уравнения вида |f(x)|=a, где

По определению абсолютной

величины, данное уравнение распадается на совокупность двух

уравнений: f(x)=a и b f(x)=-a. Записывается это так:

Причем, все решения совокупности будут решениями данного

уравнения.

Пример 3. Решить уравнение |x-4|=3. По определению модуля имеем

совокупность уравнений

откуда х1=7, х2=1.

2) Уравнения вида f(|x|)=a. По определению абсолютной величины,

данное уравнение распадается на совокупность двух систем:

3) Уравнение вида

Данное уравнение распадается на

совокупность двух систем:

Пример 4. Решить уравнение: |2x-5|=x-1. Решим сначала систему:

Затем вторую систему:

Итак, получим 2 решения х1=4 и

х2=2, которые, очевидно, удовлетворяют данному уравнению. В этом

можно убедится, сделав проверку: если х1=4, то или

|8-5|=3, т.е. |3|=3 верное тождество; если х2=2, то или

|4-5|=1, т.е. |-1|=1 - верное тождество.

4) Уравнение вида

Рассмотрим решение уравнения такого типа сразу на примере.

Пример 5. Решить уравнение |x-1|+|x-2|=1. Сначала нужно расставить на числовой оси точки, в которых подмодульные выражения обращаются в ноль. В данном случае это точки х=1 и х=2.

Нетрудно заметить, что эти точки разбивают ось на три промежутка. Далее следует определить знаки подмодульных выражений на каждом из промежутков. Итак, мы имеем

1) при (чтобы выяснить знак подмодульного

выражения, достаточно взять любую точку из указанного промежутка, например, х=0 в нашем случае и подставить в выражения х-1: 0-1= -1<0 и х-2: 0-2=-2<0). Далее, т.к. подмодульные выражения неположительны, то по определению модуля имеем: |x-1|= -x + 1 и |x-2|= -x+2.

В итоге получим: при

Точка х=1 принадлежит промежутку

следовательно, является

корнем уравнения.

2) при

имеем х-1>0,

Тогда |x-1| = x-1 и |x-2| = -x+2. Получим уравнение

х-1-х+2=1 или Уравнение имеет бесчисленное множество решений, а учитывая, что 1< x Ј 2 то делаем вывод, что решениями будут все те х, которые удовлетворяют неравенству 1< x Ј 2.

3)при х > 2 имеем |x-1| = x-1, |x-2| = x-2. Получим х - 1+х - 2 = 1 или 2х=4, откуда х = 2. Но х = 2 не принадлежит указанному промежутку, поэтому в этом случае решений нет. Окончательный ответ получим, объединив все решения. Итак, 1< x Ј 2 - все действительные числа из этого промежутка будут решениями исходного уравнения.

Пример 6. Решить уравнение | | | | x | -2| -1| -2| = 2. По определению абсолютной величины, имеем: | | | | x | -2| -1| -2| = ± 2, т.е. решаем 2 уравнения: 1) | | | x | -2| -1| = 4 и 2) | | | x | -2| -1| = 0. Решаем первое уравнение: | | | x | -2| -1| = 4 ,откуда | | | x | -2| -1| =± 4. Или | | | x | -2| = 5 и | | x | -2| = -3 (последнее уравнение решений не имеет!).

Далее, |x| - 2=± 5 или |x| = 7 и |x| = -3 (опять нет решений). Итак, |x| = 7 имеет решения x1,2 = ± 7 Решаем второе уравнение: | | | x | -2| -1| = 0. Тогда | |x| -2| -1 = 0 и | |x| -2| = 1, откуда |x| - 2 =± 1 или |x|=3 и |x|=1, откуда x3,4 = ± 3, x5,6 = ± 1. Ответ: ± 1; ± 3; ± 7.

Перейдем теперь к рассмотрению простейших графиков функций, содержащих абсолютную величину.

I. График функции y = f (|x|).

По определению модуля имеем: для х >0, y = f (x); для x <0, y = f (-x). Вообще, график функции y = f (-x) симметричен графику функции y = f (x) относительно оси oy. Следовательно, чтобы построить график функции y = f (|x|), достаточно построить график функции y = f (x) для х >0, а затем достроить его левую часть, симметрично правой относительно оси oy.

Пример 7. Построить график функции y = 2|x| -2.

а) строим график функции y = 2x - 2 для x > 0;

б) достраиваем его левую часть для x < 0, симметрично построенной относительно оси oy.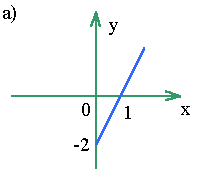

 

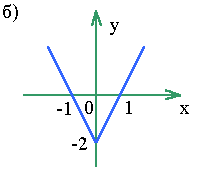
II. График функции y = | f(x) |

Под абсолютной величиной функции f(x) (т.е. под записью |f(x)|

принято понимать функцию вида:

Отсюда вытекает правило построения графиков функции y = | f(x)|:

а) строим график функции y = f (x);

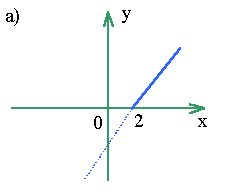
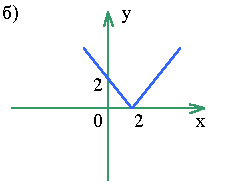
б) на участках, где график расположен в нижней полуплоскости, т.е. где f (x) <0, строим кривые, симметричные построенным относительно оси ох.

Пример 8. Построить график функции y = | x - 2 |.

а) строим график функции y = x - 2;

б) график нижней полуплоскости преобразовываем вверх симметрично оси ох.

 

III. График функции y = | f (|x|)|.

Строим график в следующей последовательности:

а) строим график функции y = f (x) для x і 0;

б) строим график функции y = f (-x) для x <0;

в) участки графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ох.

Пример 9. Построить график функции y = |1 -| x | |.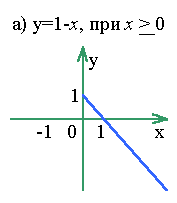

 

 

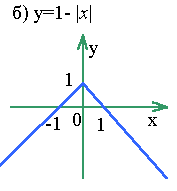
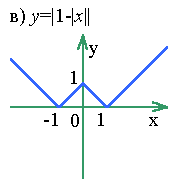
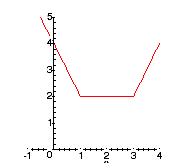
Пример 10. Построить график функции

y = |x - 1| + |x - 3| .

Точки х = 1 и х = 3 разбивают числовую ось на 3 промежутка:

  1. при x Ј 1 имеем y = -x + 1 - x + 3 = 4 - 2x;

  2. при 1< x Ј 3 имеем y = x - 1 - x + 3 = 2;

  3. при x >3 имеем y = x - 1 + x - 3 = 2x - 4.