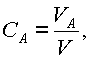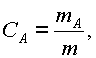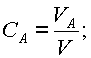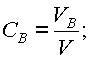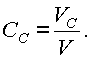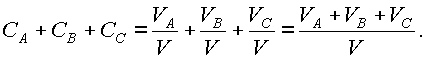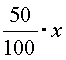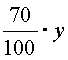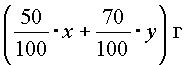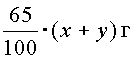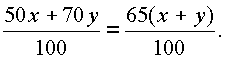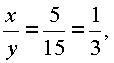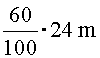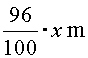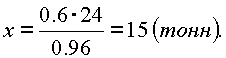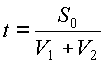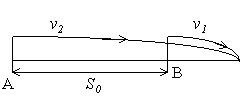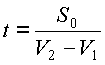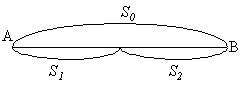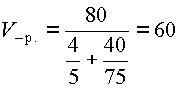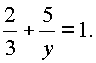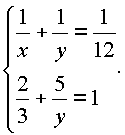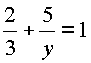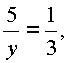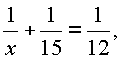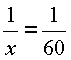7 класс
Задачи на составление уравнений
Часть 1
Составитель
: преподаватель кафедры теории функций Кубанского госуниверситета Подберезкина Анастасия Ильинична.
Среди задач на составление уравнений рассмотрим вначале те, решение которых связано с использованием понятий "концентрация" и "процентное содержание". Обычно в условиях таких задач речь идет о составлении сплавов, растворов или смесей двух или нескольких веществ. Основные допущения, как правило, принимаемые в задачах подобного рода, состоят в следующем:
- все получающиеся смеси или сплавы однородны, т.е. интересующая нас характеристика смеси одинакова для любой части смеси;
- при слиянии двух растворов, имеющих объемы V1 и V2 получается смесь, объем которой равен v1 + v2; причем последнее соотношение является именно допущением, поскольку не всегда выполняется в действительности; при слиянии двух растворов не объем, а масса смеси равняется сумме масс составляющих ее компонент.
|
Одной из наиболее распространенных характеристик смеси является |
|
концентрация конкретной составляющей смеси, т.е отношение |
|
количества этой составляющей к общему количеству смеси: |
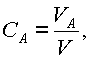
|
|
где СА - концентрация вещества А , VА - объем вещества А, V - объем всей |
|
смеси. Аналогично, |
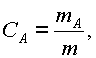
|
где mA , m - массы. |
Пример 1
. Рассмотрим смесь из трех компонент А, B, C. Покажем, что сумма концентраций всех компонент, составляющих смесь, равна 1.
|
По определению концентрации имеем: |
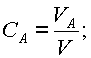
|
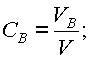
|
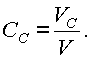
|
|
Тогда |
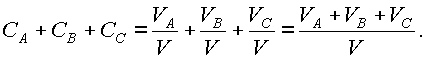
|
Заметив, что |
|
V=VA+VB+VC (см. выше допущение 2)), получим, |
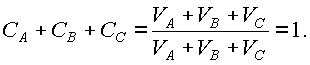
|
|
На практике концентрации принято выражать в сотых долях единицы, |
|
называемых процентами (обозначаются так - %) . |
Содержание какого-либо драгоценного металла в сплаве с примесями обычно называют пробой и обозначают числом тысячных долей единицы. Например, говоря о серебре 925 пробы, мы подразумеваем, что в каждых 1000 г такого "серебра" содержится только 925 г чистого серебра.
Пример 2. В каких пропорциях нужно смешать раствор 50-процентной и раствор 70-процентной кислоты, чтобы получить раствор 65-процентной кислоты?
Решение. Пусть мы смешаем х г раствора 50-процентной и y г раствора 70-процентной кислоты. Тогда в первом растворе содержится чистой кислоты
|
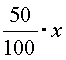
|
г, а во втором - |
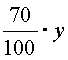
|
г. Смешав два раствора, мы получим |
|
(х+у) г смеси, в которой чистой кислоты будет |
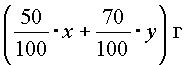
|
что |
|
должно составлять 65% от смеси, т.е. |
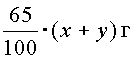
|
Таким образом , |
|
получаем уравнение: |
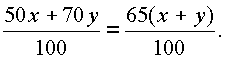
|
|
Откуда 50x+70y = 65x+65y или 5y = 15x. Таким образом, растворы нужно |
|
смешивать в пропорции 1: 3, т.к. |
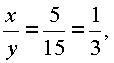
|
т.е. к 1 части 50 % -ного |
|
раствора нужно добавить 3 части 70 % -ного. |
Пример 3
. Руда содержит 40 % примесей, а выплавляемый из нее металл содержит 4 % примесей. Сколько металла можно получить из 24 т руды?
|
Решение. Пусть из 24 т руды выплавлено х т металла. Тогда количество тонн |
|
чистого металла (без примесей) будет равно |
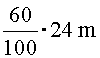
|
с одной стороны, |
|
или |
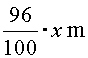
|
с другой. Имеем, таким образом, уравнение: |
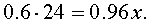
|
|
Откуда |
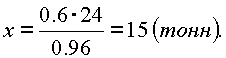
|
Ответ: можно получить 15 т металла. |
Пример 4
. За весну Обломов похудел на 25 %, затем за лето прибавил в весе 20 %, за осень похудел на 10 %, а за зиму прибавил 20 %. Похудел он или поправился за год и на сколько %?
|
Решение. Здесь в качестве неизвестного х возьмем первоначальный вес |
|
Обломова. Тогда к началу лета его вес стал (1-0,25)х = 0,75х (кг). Затем он |
|
прибавил 20% к имеющемуся весу, т.е. стал весить0,75 .(1+0,2х)= 0,75.1,2х |
|
(кг). За осень Обломов похудел на 10 %, т.е. его вес стал |
|
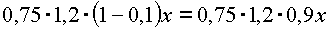
|
(кг). Учитывая, что за зиму он вновь |
|
прибавил 20 % , получим его вес к концу года |
|
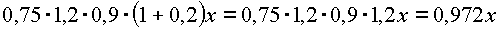
|
(кг). Т.К. его вес стал |
|
составлять 0,972 от прежнего, то делаем вывод, что за год он похудел. |
Ответ: Обломов похудел на 2,8 %.
Перейдем теперь к рассмотрению задач, условно называющихся задачами "на движение". Примем обозначения: пусть V - скорость, t - время, S - расстояние. Условимся также считать, что:
- движение на отдельных участках считается равномерным; при этом пройденный путь определяется по формуле:
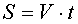
;
повороты движущихся тел принимаются мгновенными, т.е. происходят без затрат времени, скорость при этом также меняется мгновенно;
если теле движется по течению реки, то его скорость V слагается из скорости в стоячей воде Vc и скорости течения реки Vp: V = Vc + Vp, а если против течения реки, то его скорость равна V = Vc - Vp. Если в условии задачи речь идет о движении плотов, то этим хотят сказать, что тело движется со скоростью течения реки.
К задачам "на движение" относятся также и задачи, в которых кто-либо выполняет какую-нибудь работу, или задачи, связанные с наполнением и опорожнением резервуаров. В задачах такого типа работа или объем резервуаров играет роль расстояния, а производительности объектов, совершающих работу, аналогичны скоростям движения.
В задачах "на движение" полезно сделать чертеж, на котором была бы видна динамика движения с характерными моментами - встречами, остановками и поворотами.
При решении задач "на движение" часто встречаются следующие два элемента:
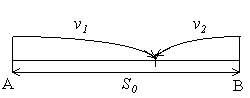
1) движение навстречу друг другу; если первоначальное расстояние между двумя точками, движущимися навстречу друг другу со скоростями V
1 и V2 , равно S0, то время, через которое они встретятся,
|
равно |
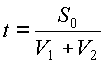
|
(находится из уравнения V 1t+V2t=S0). |
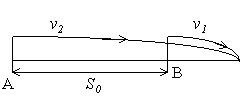
2) движение в одном направлении; если первоначальное расстояние между двумя точками, из которых одна догоняет другую, равно S
0 , то время, через которое вторая точка (скорость V2) догонит первую
|
(скорость V1) равно |
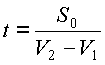
|
(V2>V1 ) (находится из уравнения |
V2t-V1t = S0).
Пример 5
. Коля шел домой вверх по течению ручья со скоростью в 1,5 раза большей, чем скорость течения, и держал в руках шляпу и палку. На ходу он бросил в ручей шляпу, перепутав ее с палкой. Вскоре, заметив ошибку, он бросил палку в ручей и побежал назад со скоростью вдвое большей той, с какой шел вперед. Догнав плывущую шляпу, он мгновенно достал ее из воды, повернулся и как ни в чем ни бывало пошел домой с прежней скоростью. Через 40 сек. после того, как он догнал шляпу, он встретил палку, плывущую ему навстречу. Насколько раньше пришел бы он домой, если бы все время шел вперед? 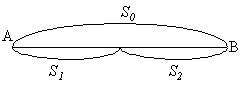
Решение. Пусть Коля бежал назад t секунд. Тогда палка плыла назад (t+40) секунд. Пусть V - скорость течения. Тогда скорость ходьбы 1,5V, бега 3V. S
0 - расстояние, которое он бежал назад, S1 - расстояние которое плыла палка до встречи с ним, S2 - расстояние, которое Коля шел вперед, выловив шляпу. S0=S1+S2. Учитывая, что S0=3Vt;
|
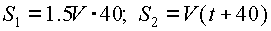
|
, получаем уравнение: |
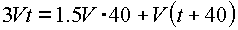
|
|
3Vt=60V+Vt+40V 2Vt=100V t=50 (сек). Время, которое Коля потерял, равно |
|
50 секунд плюс время, которое ему потребовалось, чтобы пройти то же |
|
расстояние, а оно вдвое больше. Всего получается Всего получается |
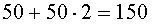
|
секунд.
Ответ: 2,5 мин. потерял Коля.
Пример 6. Грузовик проехал расстояние 80 км. Первую половину пути он ехал со скоростью 50 км/ч, а вторую половину - со скоростью 75 км/час. Найдите среднюю скорость движения грузовика.
Решение. Для нахождения средней скорости нужно разделить пройденный путь на все затраченное время. На прохождение первых 40 км пути грузовик затратил 40/50 часа, а на прохождение оставшихся 40 км - 40/75 часа. Тогда
|
средняя скорость равна |
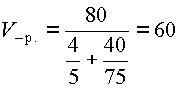
|
км/час. |
Замечание.
В разобранном примере было бы ошибкой считать среднюю скорость как полусумму скоростей движения на двух участках. Так нельзя делать потому, что время прохождения одинаковых по протяженности участков различно! Грузовик дольше ехал с меньшей скоростью, поэтому средняя скорость получается меньше полусуммы скоростей.
Пример 7. Двое рабочих, работая вместе, могут окончить некоторую работу в 12 дней. После 8 дней совместной работы один из них заболел, и другой окончил работу один, проработав еще 5 дней. Во сколько дней каждый из них, работая отдельно, может выполнить эту работу?
|
Решение. Пусть один рабочий может выполнить работу в х дней, а другой в y |
|
дней. Каждый из них выполняет в день |
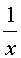
|
и |
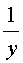
|
части работы |
|
соответственно, а работая вместе |
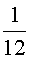
|
часть. Получаем уравнение: |
|

|
За 8 дней совместной работы они выполнили |
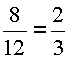
|
всей |
|
работы. Другой рабочий работал еще 5 дней, выполнив |
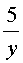
|
часть всей |
|
работы. Зная, что вся работа была сделана, составим уравнение: |
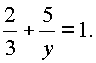
|
|
Итак, имеем систему уравнений |
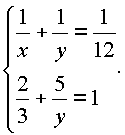
|
Решением системы |
|
являются такие |
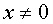
|
и |
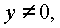
|
которые удовлетворяют как первому, |
|
так и второму уравнению. Из уравнения |
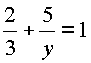
|
найдем y: |
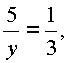
|
|
y=15. Подставим в 1-е уравнение: |
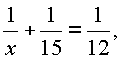
|
откуда |
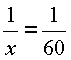
|
и х=60. |
Ответ: х=60; y=15 дней.
Литература.
1. Алгебра 7 класс, под редакцией Теляковского С.А.
2. Лурье М.В., Александров Б.И.. Задачи на составление уравнений.