§ 4. ИСПОЛЬЗОВАНИЕ СВОЙСТВ ЗАМЕЧАТЕЛЬНЫХ ЛИНИЙ В ТРЕУГОЛЬНИКЕ И ДРУГИХ ТЕОРЕМ
Конечно, при решении задач на площади может понадобиться любая из известных вам теорем. В частности, иногда удобно применять свойства биссектрис и медиан, которые доказаны в примере 6 и следствии 2.
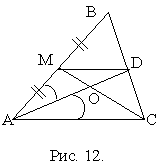
Пример 7. В треугольнике АВС проведены биссектриса
AD и медиана СМ, пересекающиеся в точке О. Известно, что АВ=6, ВС=4, АС=5. Найти отношение
:
.
Решение
. Согласно примеру 6 имеем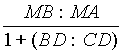
= 
= 
; 
= 
= 
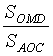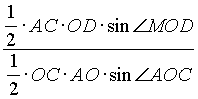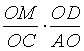. По теореме 1 
= 
= 
= 
. Следовательно, 
= 
= 
= 
= 
.
Ответ:
:=11 : 3.
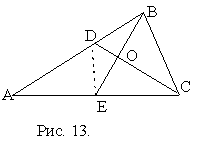
Пример 8
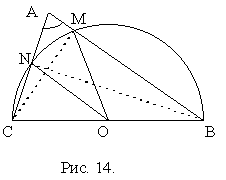
. В треугольнике АВС биссектриса CD и медиана ВЕ перпендикулярны (рис. 13), причем ВЕ=m, CD=l. Найти площадь треугольника АВС.Решение
. Пусть О - точка пересечения ВЕ и CD. Поскольку Р ВСО = Р ЕСО и ВЕ ^ СО, то треугольник ВСЕ - равнобедренный и ВО = ОЕ =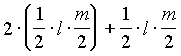
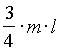. Поскольку АЕ = СЕ, то 
= 
. Следовательно, 
= ++
= +
= 
= 
.
Ответ:
= .
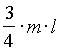Как и во многих других геометрических задачах на площади помогает выделение подобных фигур. Известно, что отношение площадей подобных фигур с коэффициентом подобия
k равно k2. Если, например, радиус одной окружности в 3 раза больше радиуса другой, то отношение площадей равно 9.Пример 9. В треугольнике АВС угол
Р ВАС=60О, ВС=2R, точка О - середина ВС. На стороне ВС как на диаметре построена окружность радиуса R, пересекающая сторону АВ в точке М, а сторону АС - в точке N. Известно, что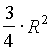
+
= 
. Найти .
Решение
. Проведем отрезок СМ. Поскольку вписанный угол Р СМВ опирается на диаметр ВС, то Р СМВ =90О и треугольник АМС - прямоугольный. Так как Р САВ =90О, то АС=2АМ. Аналогично, АВ=2АN. Таким образом, треугольники NAM и ВАС подобны (Р ВАС =Р NAM,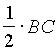
= = 
) с коэффициентом подобия и MN= 
= R. Из подобия треугольников NAM и ВАС следует, что 
:
= 
= 
. Поскольку МО и NO - радиусы нашей окружности радиуса R, то треугольник MON - равносторонний и 
= 
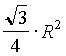. Таким образом, = (
+
)++=
++
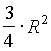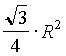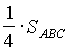и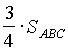 
= += 
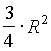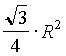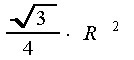. Следовательно, =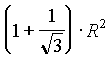 
Ответ:
= .
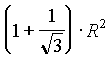Если на чертеже есть параллельные прямые, то у нас зачастую появляется возможность применить теорему Фалеса или теоремы о параллелограммах, или обнаружить подобные треугольники. Иногда достаточно провести через нужную точку прямую, параллельную какому-то отрезку, чтобы решение задачи стало прозрачным. Так мы делали в примере 2.
Пример 10. Треугольник АВС - равнобедренный (АВ
=ВС). Точка О - середина высоты BD. Прямая АО пересекает ВС в точке К (рис. 15). Площадь треугольника АВС равна 1. Найти площади треугольников АОС, КОС и ВОК.Решение
. Очевидно,
= 
= 
= 
= 
= .
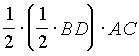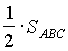Поскольку ВО
= OD, то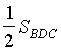
= 
= 
= 
= 
.
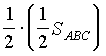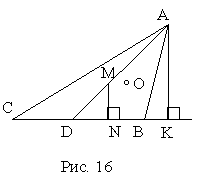
Проведем через точку
D отрезок DM, параллельный АК (рис. 15). Так как AD = DC, то DM - средняя линия треугольника АКС и КМ = МС. Поскольку ВО = OD, то ОК - средняя линия треугольника ВМD и ВК = КМ. Следовательно, КМ = МС = ВК и ВК =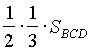
ВС. Но тогда согласно свойству 5, 
=
= 
, 
= -= 
.
Ответ:
=
, = , = .
Пример 11
. Длины сторон треугольника АВС образуют арифметическую прогрессию и АВ < ВС < АС. Доказать, что тогда центр окружности, вписанной в в этот треугольник, и точка пересечения его медиан лежат на прямой, параллельной ВС.Доказательство
. Пусть AD - медиана, М - точка пересечения медиан, О - центр вписанной окружности (рис. 16). Нам нужно доказать, что расстояние MN от М до ВС равно радиусу окружности, вписанной в треугольник АВС.Опустим из точки А высоту АК на ВС. По следствию 2 из теоремы 3 имеем 3МD
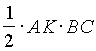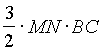=AD. Отсюда и из подобия треугольников MND и АКD (Р ADK=Р MND, Р AKD=Р MND=90O) получаем, что 3MN=АК. По формуле (3) площади треугольника имеем=pr, где р=(АВ+ВС+АС)= 
ВС (поскольку ВС - среднее арифметическое между АВ и АС). С другой стороны, = 
=
. Сравнивая эти выражения, получаем 
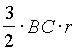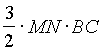= и MN = r.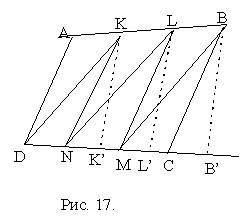
Пример12
. В четырехугольнике ABCD на стороне АВ выбраны точки К и L, а на стороне CD - точки M и N так, что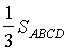
АВ= АК= КL= LB; CD= CM= MN= ND (рис. 17). Доказать, что 
= 
.
Доказательство
. Покажем сначала, что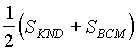
= 
. Опустим из точек K, L, B перпендикуляры КК', LL' и BB' на прямую CD. Эти перпендикуляры параллельны между собой и KL = LB. Следовательно, по теореме Фалеса, LL' - средняя линия трапеции KBB'K' и LL'=(КК'+BB'). Учитывая еще, что DN=NM=MC, имеем: 
= 
= 
= 
= .
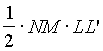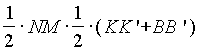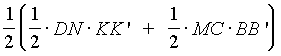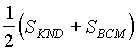Точно так же доказывается, что
.
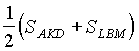Таким образом,
+=
= 
= 
.
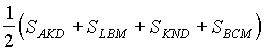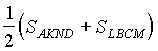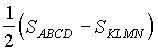Из полученного равенства
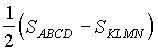легко выразить 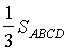= , что и требовалось.
Internet-school | Условия задач | Методические указания | Наши адреса | Правила оформления рукописей