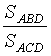 =
= 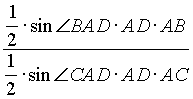 =
= § 3. ПРИМЕНЕНИЕ ФОРМУЛ ДЛЯ ВЫЧИСЛЕНИЯ ПЛОЩАДИ ТРЕУГОЛЬНИКА ПРИ РЕШЕНИИ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ
Как вы заметили из формул (1)-(5), площадь треугольника довольно просто выражается через разнообразные комбинации элементов этого треугольника. Поэтому сравнение различных выражений для площади треугольника позволяет иногда решать задачи, на первый взгляд не связанные с понятием площади. Мы так уже поступали в примере 4. Приведем одно из доказательств следующего известного вам факта.
Пример 6. Доказать, что отношение длин отрезков, на которые биссектриса
AD треугольника ABC делит сторону BC, равно отношению AB:AC.Доказательство
. Рассмотрим отношение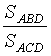 =
= 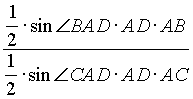 =
= ![]() . Следовательно,
. Следовательно, ![]() =
= ![]() , что и требовалось.
, что и требовалось.
Приведем еще примеры.
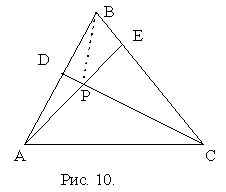
Теорема 1. Пусть в треугольнике ABC на сторонах AB и BC выбраны соответственно точки D и E, а точка Р является точкой пересечения отрезков AE и CD (рис. 10). Если ВЕ:СЕ= a , ВD:AD= b , то ![]() =
= ![]() ;
; ![]() =
= ![]() .
.
Доказательство
. Проведем отрезок BP. По свойству 2,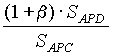 = a ; т.е.
= a ; т.е. 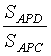 =
= 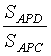 =
= Теорема 2
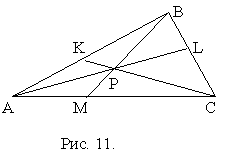
. (Теорема Чевы). Пусть на сторонах AB, BC и AC треугольника ABC выбраны точки K, L и M соответственно так, что отрезки AL, BM и CK пересекаются в одной точке Р (рис. 11). Тогда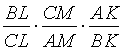 =1.
=1.
Доказательство
. По свойству 4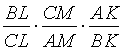 =
= 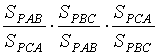 =1. Теорема доказана.
=1. Теорема доказана.
Справедливо и обратное к теореме Чевы утверждение:
Теорема 3. Пусть на сторонах
AB, BC и AC треугольника ABC выбраны точки K, L и M соответственно так, что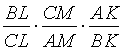 =1. Тогда отрезки AL, BM и CK пересекаются в одной точке.
=1. Тогда отрезки AL, BM и CK пересекаются в одной точке.
Доказательство. Пусть
AL и BM пересекаются в некоторой точке Q. Допустим, что прямая CQ пересекает AB в точке N. Согласно теореме Чевы необходимо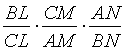 =1. Но по условию теоремы
=1. Но по условию теоремы 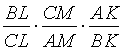 =1. Следовательно,
=1. Следовательно, На важность теоремы Чевы и обратной к ней указывают легко получающиеся из нее следствия.
Следствие 1. Высоты любого остроугольного треугольника пересекаются в одной точке.
Доказательство. Пусть
AL, BM и СК - высоты остроугольного треугольника ABC. Тогда BL=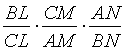 =
= 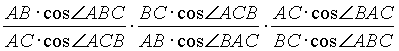 =1, и по теореме 3 отрезки AL, BM и CK пересекаются в одной точке.
=1, и по теореме 3 отрезки AL, BM и CK пересекаются в одной точке.
Следствие 2. Медианы любого треугольника пересекаются в одной точке и каждая из них делится точкой пересечения в отношении 2:1, считая от вершины треугольника.
Доказательство. Пусть точки
K, L и M являются серединами сторон AB, BC и АС соответственно треугольника АВС. По теореме 3 отрезки AL, BM и CК пересекаются в одной точке Р. По свойствам 2 и 4 имеемЗамечание. Следствие 2 можно легко вывести также из теоремы 1.
Internet-school | Условия задач | Методические указания | Наши адреса | Правила оформления рукописей