ЗОНАЛЬНАЯ ОЛИМПИАДА ПО МАТЕМАТИКЕ
1997 - 1998 уч.г. 11 класс задания
- Прямые m и n, пересекающие боковые стороны AB и CD трапеции ABCD , параллельны ее основаниям AD и ВС. Докажите, что полоса, ограниченная прямыми m и n, отсекает на углах BAC и BDC равновеликие фигуры.
- На клетчатой бумаге отмечен прямоугольник s х r клеток. Двое играют в такую игру. Они по очереди должны вычеркивать какую-то строку или какой-то столбец (если в них есть еще не вычеркнутые клетки). Выигрывает тот, кто вычеркнул последнюю клетку. Кто при правильной стратегии может обеспечить себе победу - начинающий или его партнер?
- Найти все целые решения уравнения
y2 = x3 - 3x+2
.
- Найти сумму наибольшего и наименьшего решений уравнения
(х+1)7 + (х-1)7 = sin 5х - 4sin3х
- 4sin3х
- Найти все последовательности
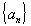
, удовлетворяющие условию
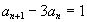
![]() - 4sin3х
- 4sin3х![]()