1997 - 1998 уч.г.11 класс, решения

1. Пусть О - точка пересечения диагоналей и l - прямая, проходящая через О параллельно AD. Сначала докажем, что l отсекает на углах BAC и BDC равные отрезки. Затем, используя подобие треугольников, покажем, что каждая из прямых m и n тоже отсекает на этих углах равные отрезки. И, наконец, замечаем, что отсекаемые полосой на данных углах фигуры - равновеликие трапеции.
1. Начинающий выигрывает при четных s и r, а также при нечетных s и r. В других случаях выигрывает партнер.
2. x=0; x=n² - 2, где n= 0,1,2,...
3. 0, ввиду нечетности выражения.
4. x_n= 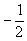; x’_n = aЧ3ⁿ - 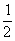, где а - const.