КРАЕВАЯ ОЛИМПИАДА ПО МАТЕМАТИКЕ

1997 - 1998 уч. г. 9 класс

задания

1 день

  1. В полдень из пункта А в пункт Б выехал "Москвич". Одновременно из Б в А по той же дороге выехали "Жигули". Через час "Москвич" находился на полпути от А до "Жигулей". Когда он окажется на полпути от "Жигулей" до Б (скорости автомобилей постоянны)?

  2. Доказать, что n5-5n3 +4n делится на 120, если n - натуральное число.

  3. Имеет ли уравнение x1997 + 2x1996 +3x1995 +...+1997x+1998=0 целые корни?

  4. Параллельно основанию AD трапеции ABCD (BD- диагональ) проведена прямая 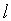так, что сумма площадей трапеций FDAE и FBCG принимает наибольшее возможное значение, где E, F, G -точки пересечения прямой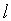

с отрезками AB, BD, DC . Докажите, что точки A,F,C лежат на одной прямой.

 

КРАЕВАЯ ОЛИМПИАДА ПО МАТЕМАТИКЕ

1997 - 1998 уч. г. 9 класс

задания

2 день

  1. Разложить на множители (b-c)3 +(c-a)3 +(a-b)3.

  2. Доказать, что графики функций y=x3-3a2 x и y=x3-3ax2 получаются один из другого сдвигом.

  3. Доказать, что для любых положительных a, b, c справедливо неравенство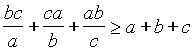

  4. Найдите наибольшее число 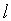такое, что при любой раскраске единичного квадрата в два цвета, внутри него найдется отрезок с одноцветными вершинами длины не меньше, чем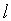

.