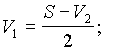
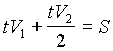 . Перепишем оба уравнения в виде:
. Перепишем оба уравнения в виде: 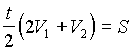 . Отсюда следует, что
. Отсюда следует, что КРАЕВАЯ ОЛИМПИАДА ПО МАТЕМАТИКЕ
9 класс
решения
1 день
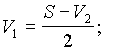
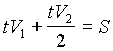 . Перепишем оба уравнения в виде:
. Перепишем оба уравнения в виде: 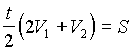 . Отсюда следует, что
. Отсюда следует, что ![]() .
.
z
- расстояние между прямымиИмеем
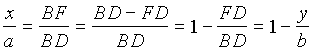 , откуда
, откуда 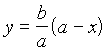 . Кроме того,
. Кроме того, 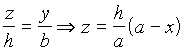 .
.
Теперь
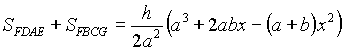 принимает наибольшее значение при
принимает наибольшее значение при 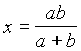 , тогда
, тогда 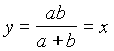 .
.
Далее, из
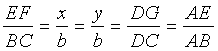 и
и 2
деньТ.к.
1) При любой раскраске найдутся две одноцветные точки квадрата на расстоянии не меньшем, чем
 - противоречие. Значит,
- противоречие. Значит, 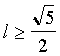 .
.
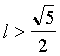 . Проведем прямую через
. Проведем прямую через 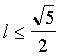 .
.