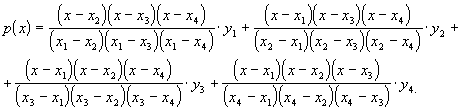КРАЕВАЯ ОЛИМПИАДА ПО МАТЕМАТИКЕ

1997-1998 уч. г. 11 класс

решения

1-й день

1.

.

2.

.

3.

  1. В первой и третьей четверти решений нет.

1) Пусть

. Тогда

т. е.

Тогда

Случай n = 0 и n = 1 невозможен, т.к. тогда

При

Получаем, что n = 2.

Из этого следует

или, что то же,

Теперь получаем

и, значит,

.

2) Пусть

т.е.

и, значит,

Ответ:

2 день.

  1. Пусть О - центр описанного шара . Из О опустим на ASC Т.к. наклонные к этой грани OA, OC, OSравны между собой как радиусы шара, то проекции этих наклонных равны между собой: AK=CK=SK. Следовательно, К - центр описанного вокруг грани ASC круга. Но из того, что - прямоугольный, следует, что К – середина АС. Теперь заметим, что ребро BS параллельно OK, т.к. BS и OK перпендикулярны грани ASC. Проведем через параллельные OK и BS плоскость OKSB. Эта плоскость содержит прямую SO и медиану BK основания ABC. Аналогично доказывается, что прямая OL параллельна ребру AS. Эти прямые определяют плоскость OLSA, которая также содержит прямую SO и другую медиану AL основания ABC. Итак, медиана AL и BK основания ABC принадлежат двум плоскостям, пересекающимся по прямой SO. Следовательно, точка G пересечения медиан основания пирамиды лежит на прямой SO, что и требовалось доказать.

  2. Да, существуют. Например:

где

– различные простые

числа.

7.

убывает на промежутке

, при этом

Значит, существует

единственное

такое, что

На

на

. Т.к.

и т.к. на первом

промежутке f(x) возрастает, а на втором убывает, получаем, что

f(x) > 0 для