КРАЕВАЯ ОЛИМПИАДА ПО МАТЕМАТИКЕ

1997 - 1998 уч.г.10 класс

решения

1 день

  1. Количество спирта, попавшее в “совместную” бутыль за 1 час равно

общее количество спирта

Ответ: 72%.

2.Пусть x0 >1998 – корень уравнения. Тогда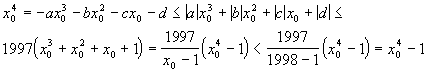

Итак,

Противоречие. Значит, такого корня нет.

  1. Искомая парабола не перпендикулярна оси и поэтому ее уравнение

    2. можно записать в виде y = kx + b. Уравнение

    имеет два различных корня при условии:

    Т.к. последнее неравенство должно выполняться при всех ненулевых значениях а, то b = 2k – 1,то Но полученная нами прямая y=kx+2k–1 должна проходить через точку (1997; 1998), поэтому k = 1. Итак, искомая прямая y = x + 1 и она единственна.

     

  2. Опустим из точки М – середины стороны АС – перпендикуляры на

стороны ВС и АВ.

, но т.к.

, то

Значит

. Точно так же есть половина высоты СD,

При этом

. Значит,

меньше

.

Следовательно,

меньше

.

2 день

5.

Пусть

, где

, перепишем наше равенство

в виде

.

Значит, либо

либо

.

Рассмотрим первую систему неравенств

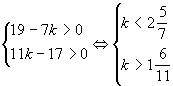
и .

Рассмотрим вторую систему неравенств

.

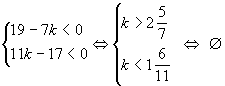Ответ: n=1.

  1. Внутри окружности имеются две горизонтальные параллельные хорды. С помощью линейки легко найти на каждой из них их середины. Прямая, проходящая через эти середины, проходит через центр окружности. Аналогично поступаем и с парой вертикальных параллельных хорд, лежащих внутри окружности. Прямая, проходящая через пару этих новых середин, проходит и через центр окружности. Точка пересечения найденных прямых и является искомым центром.

7. Воспользуемся неравенством

8. Пусть гирьки и их массы обозначены по ходу часовой стрелки

буквами

начиная с некоторого места.

На левую чашку: A и С, на правую: F и G.

  1. A + C > F + G, тогда? D, E, F.

    2. a)

    б)

    в)

    .

  2. A + C < F + G рассмотрим аналогично

  3. A + C = F + G? B, C, G

a)

б)

в)