1. Дано m положительных чисел. Известно, что произведение любых n из них больше 1. Доказать, что произведение всех этих чисел больше 1.

2. У трех братьев - Андрея, Василия и Сергея - дни рождения совпадают. Когда старшему из них, Андрею, исполнилось 12 лет, то оказалось, что сумма возрастов всех трех братьев делится на 12. То же случилось, когда 12 лет исполнилось Василию. Докажите, что то же самое случится, когда 12 лет исполнится Сергею.

3. Лучи a, b, c имеют общее начало D и луч с делит угол (ab) в отношении 2:1. Через точку D проведена окружность, которая пересекает луч a и дополнительные лучи к лучам b и с в точках A, B, C соответственно и так, что АС - биссектриса угла BAD. Докажите, что четырехугольник ABCD - либо квадрат, либо равнобедренная трапеция.

4. Найти наименьшее натуральное число n, такое чтобы числа 2n+1 и 37n+1 были квадратами некоторых целых чисел.

1. В равнобедренном треугольнике АВС боковые стороны АВ и ВС равны а. На основании АС взяты точки М и К так, что угол МВК равен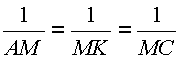 . Найти МВ, если .

2. Доказать, что для любых действительных чисел a, b, c справедливо неравенство (a+b+c)2<3(a2+b2+c2).

3. В клетки таблицы m x n вписаны некоторые числа. Разрешается одновременно менять знак у всех чисел некоторого столбца или некоторой строки. Доказать, что применяя несколько раз эту операцию, можно превратить данную таблицу в такую, у которой суммы чисел, стоящих в любой строке и в любом столбце, неотрицательны.

4. Дано уравнение . Показать, что если , (где r, s - некоторые натуральные числа) таковы, что , то (r, s) - целочисленные решения данного уравнения.