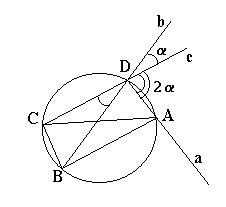
Пусть дуга СВ равна 2
a. Тогда дуга CD равна 2a и дуга DA равна 2a. Значит, отрезки ВС, CD и AD равны. При ВС параллельном AD имеем квадрат, а при ВС не параллельном AD - равнобедренную трапецию.Ответы и указания к задачам краевой математической олимпиады 1996 года
IX класс
1 день
1. Очевидно.
2. Имеем три ситуации:
1) 12, 12
-х, 12-у;2) 12
+х, 12, 12+х-у;3) 12
+у, 12+у-х, 12.Первая соответствует тому времени, когда Андрею было 12 лет; вторая - когда Василию было 12 лет, третья - когда Сергею стало 12 лет. Первый случай дает нам: х+у делится на 12; второй дает: 2х-у делится на 12. В третьем случае 2у-х=
(х+у)-(2х-у).3.
|
|
Пусть дуга СВ равна 2 a. Тогда дуга CD равна 2a и дуга DA равна 2a. Значит, отрезки ВС, CD и AD равны. При ВС параллельном AD имеем квадрат, а при ВС не параллельном AD - равнобедренную трапецию. |
4. При 2
n+1=m2, 37n+1=k2 имеем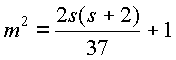 , где s+1=k. Отсюда легко увидеть, что искомое n получается при s=72, оно равно 144.
, где s+1=k. Отсюда легко увидеть, что искомое n получается при s=72, оно равно 144.
2 день
1. Пусть ВD - высота, МВ=х, MD=y. Тогда МК=![]() , АМ=
, АМ=![]() , MC=
, MC=![]() . Из условия задачи теперь следует, что х=
. Из условия задачи теперь следует, что х=![]() .
.
2. Воспользоваться неравенством
a2+b2+c2>ab+bc+ac.3. Следует обратить внимание на то, что:
1) сумма абсолютных величин всех чисел, вписанных в таблицу, конечна.
2) одновременной сменой знаков у чисел, находящихся в столбцах или строках, можно добиться того, чтобы сумма
S всех чисел новой таблицы была неотрицательной;3) если какой-нибудь столбец (или строка) имеет отрицательную сумму, то одновременная смена знаков у всех его элементов приводит к возрастанию
S.4. Очевидно,
r1=3, s1=2 являются решениями уравнения. a=3+2