ЗАДАЧИ КРАЕВОЙ МАТЕМАТИЧЕСКОЙ ОЛИМПИАДЫ 1996 год
XI класс
1 день
1
. Угол между боковым ребром и основанием правильной четырехугольной пирамиды равен2
. В остроугольном треугольнике ABC высоты пересекаются в точке О. Доказать, что радиусы окружностей, описанных вокруг треугольников АВС, АОВ, АОС, ВОС равны между собой.3
. При любом натуральном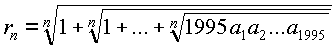 , причем данное выражение содержит
, причем данное выражение содержит 4
. Для положительных чисел а1,а2,...,аn доказать неравенство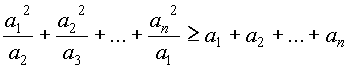 .
.
2 день
1
. Решить неравенство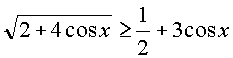 .
.
2
. Пусть дана парабола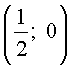 находится точечный источник света, всякий луч которого, достигая параболы, отражается от нее в соответствии с законом физики: "угол падения равен углу отражения". Доказать, что все отраженные лучи будут горизонтальными.
находится точечный источник света, всякий луч которого, достигая параболы, отражается от нее в соответствии с законом физики: "угол падения равен углу отражения". Доказать, что все отраженные лучи будут горизонтальными.
3
. Пусть на окружности с центром в точке О радиуса 1 взята произвольная точка М. На луче OS, выходящем из О, взяты точки P и Q на расстоянии r и4
. Пусть а1,а2,...,аn и b1,b2,...,bn - две последовательности положительных чисел, причем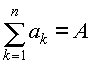 ,
, 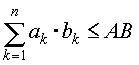 . Тогда
. Тогда 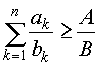 .
.