 .
.ЗАДАЧИ КРАЕВОЙ МАТЕМАТИЧЕСКОЙ ОЛИМПИАДЫ 1996 год
X класс
1 день
1
. Решить уравнение:2
. Точка, находящаяся на числовой оси, может передвигаться в положительном направлении с шагома) Доказать, что при любых различных
m, n О Z точка за несколько шагов может попасть из m в n.б) При
k=5 найдите наименьшее возможное число шагов, за которые можно попасть из 1945 в 1996.3
. Дан прямоугольник со сторонами4
. Найдите функцию f(x), если она определена для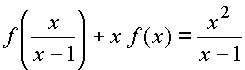 .
.
2 день
1
. Сколько отрицательных корней имеет уравнение2
. На каждой стороне параллелограмма взято по точке. Площадь четырехугольника с вершинами в этих точках равна половине площади параллелограмма. Доказать, что хотя бы одна из диагоналей четырехугольника параллельна стороне параллелограмма.3
. Пусть при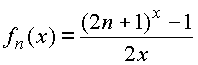 , где nОN. Доказать, что каждая прямая
, где nОN. Доказать, что каждая прямая 4
. Пусть a, b, c – натуральные числа. Доказать, что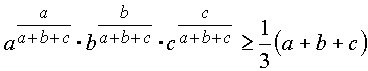 .
.