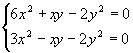
не имеет решений в натуральных числах.
Существует ли правильный треугольник с вершинами в узлах сетки?
|
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И |
ЗОНАЛЬНАЯ ОЛИМПИАДА ПО МАТЕМАТИКЕ 1998 - 1999 учебный год 10 класс задания Председатель предметно-методической комиссии: доцент КубГУ Антонюк Г.К. |
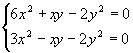
не имеет решений в натуральных числах.
Существует ли правильный треугольник с вершинами в узлах сетки?
На плоскости даны 9 точек, никакие три из которых не лежат на одной прямой. Докажите, что из них можно выбрать такие две четверки точек, что точки каждой из этих четверок являются вершинами двух выпуклых четырехугольников. При этом один четырехугольник содержит внутри себя второй четырехугольник.