350088 г. Краснодар, ул. Сормовская 203
Центр дополнительного
образования
тел. (8612) 32-99-04
Председатель предметно-методической комиссии по математике, доцент КубГУ
Антонюк Г.К.

КРАЕВАЯ ОЛИМПИАДА
ПО МАТЕМАТИКЕ

1998-1999 уч.г.
10 класс, 2 день
Ответы.

  1. Сумма коэффициентов равна 1.

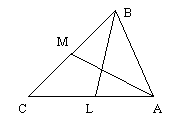
  2. ABM – равнобедренный треугольник, AB = BM. Положим AB = n, тогда ВС = 2n, а длина m третьей стороны удовлетворяет неравенству: n < m < 2n. Поэтому существует ровно 2n-1 различных треугольников с наименьшей стороной, равной n. Учитывая, что n < 1999, находим общее число треугольников как сумму 1999 членов арифметической прогрессии с an = 2n-1. Ответ: 19992.

  3. Разделим все части неравенства на а и положим b/a = х. Тогда неравенство примет вид:

< < ; (0 < x < 1). Перепишем неравенства в виде:

< < ;

или

< 1< .

  1. ;

  2. 4х = .

  1. Пусть А1, В1, С1 – середины сторон ВС, АС и АВ соответственно. Для треугольника АВС предполагаем, что R = 2r. DА1В1С1 подобен DАВС и поэтому r = R/2, где r - радиус окружности, описанной около DА1В1С1. Если эта окружность не касается некоторых сторон DАВС, то проведем касательные, параллельные этим сторонам, к соответствующим дугам этой окружности, выходящим за пределы треугольника. Получим DА2В2С2, подобный DАВС и имеющий большую площадь… и r - радиус окружности, вписанной в DА2В2С2. Тогда r > r, но r = R/2 и получаем: r > R/2. Противоречие. Значит, построенная описанная около DА1В1С1 окружность, касается сторон DАВС. Теперь легко установить, что он – равносторонний.