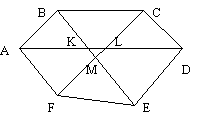
 Ответ: 1999:1998. Это легко следует из того, что будет нами доказано: диагонали AD, BE и CF пересекаются в одной точке. Треугольники AKB и DKE равновелики (если К – точка пересечения диагоналей AD и BE), CLD и FLA тоже равновелики и EMF и BMC тоже равновелики (где L и M – соответствующие точки пересечения). Поэтому имеем три равенства: АК . ВК= DK . EK, CL . DL= FL . AL и EM . FM= BM . CM. Перемножив их, получим AK . BK . CL . DL . EM . FM = AL . BM . CM . DK . EK . FL. Это равенство противоречит рисунку, из которого видно, что каждый множитель в левой части меньше соответствующего множителя в правой части равенства.
Ответ: 1999:1998. Это легко следует из того, что будет нами доказано: диагонали AD, BE и CF пересекаются в одной точке. Треугольники AKB и DKE равновелики (если К – точка пересечения диагоналей AD и BE), CLD и FLA тоже равновелики и EMF и BMC тоже равновелики (где L и M – соответствующие точки пересечения). Поэтому имеем три равенства: АК . ВК= DK . EK, CL . DL= FL . AL и EM . FM= BM . CM. Перемножив их, получим AK . BK . CL . DL . EM . FM = AL . BM . CM . DK . EK . FL. Это равенство противоречит рисунку, из которого видно, что каждый множитель в левой части меньше соответствующего множителя в правой части равенства.